Равнобедренный треугольник. Готовимся к ОГЭ по математике. Модуль 2. Урок 48

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна стороне треугольника и равна её половине. $\displaystyle MN\parallel AC,MN=\frac{1}{2}AC$ (см. рис.1).

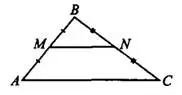
Рис.1

Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины. На рисунке 2 получаем
$\displaystyle \frac{CO}{C_{1}O}=\frac{BO}{B_{1}O}=\frac{AO}{A_{1}O}=\frac{2}{1}$.
Например, если $\displaystyle BB_{1}=12$, то $\displaystyle BO=\frac{2}{3}BB_{1}=12\cdot \frac{2}{3}=8$ и $\displaystyle OB_{1}=\frac{1}{3}BB_{1}=4$.
Прямые, содержащие высоты треугольника, пересекаются в одной точке.

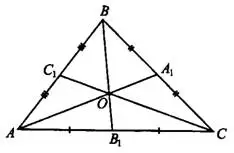
Рис.1

Биссектрисы треугольника пересекаются в одной точке. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Равнобедренный и равносторонний треугольники

Треугольник называется равнобедренным, если две его стороны равны. Они называются боковыми сторонами. Третья сторона называется основанием. На рисунке 3 $\displaystyle AB=BC$, $AC$ — основание $\displaystyle \bigtriangleup ABC$.

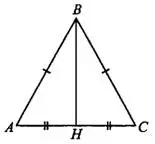
Рис.3

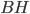В равнобедренном треугольнике углы, прилежащие к основанию, равны ($\displaystyle \angle BCA=\angle BAC$ на рисунке 3), а высота, медиана и биссектриса, проведённые к основанию, совпадают. $BH$ является одновременно и медианой, и биссектрисой, и высотой в $\displaystyle \bigtriangleup ABC$ на рисунке 3.
Если в треугольнике два угла равны, то этот треугольник равнобедренный. На рисунке 4 $\displaystyle \angle ABC=\angle ACB$, а значит, $\displaystyle \bigtriangleup ABC$ - равнобедренный ($\displaystyle AB=AC$).

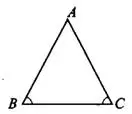
Рис.4

Треугольник называется равносторонним, если все его стороны равны. Равносторонние треугольники также называют правильными.
В равностороннем треугольнике все углы равны 60°, а медиана, биссектриса и высота, проведённые к любой из его сторон, совпадают.
Если в треугольнике все углы равны, то треугольник равносторонний.
Задача 1. Найдите сторону 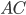$AC$ треугольника $ABC$, если $\displaystyle \angle BAC=120^{\circ},\angle ABC=30^{\circ}$, а $\displaystyle AB=5$.
Решение.
$\displaystyle \angle ACB=180^{\circ}-\angle BAC-\angle ABC=180^{\circ}-120^{\circ}-30^{\circ}=30^{\circ}=\angle ABC$,
значит, $\displaystyle \bigtriangleup ABC$ - равнобедренный и $\displaystyle AC=AB=5$ (см. рис. 5).

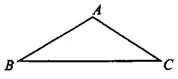
Рис.5

Ответ: 5.
Задача 2. Медианы $\displaystyle AA_{1}$ и $\displaystyle BB_{1}$ треугольника $ABC$ пересекаются в точке $O$. Найдите $AO$, если $\displaystyle AA_{1}=6$.
Решение.
$O$ — точка пересечения медиан (см. рис.6).

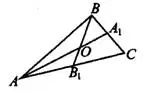
Рис.6

$\displaystyle \frac{AO}{OA_{1}}=\frac{2}{1}=2,AO=2OA_{1},AO+A_{1}O=AA_{1}=6,$
$\displaystyle 2OA_{1}+OA_{1}=6,3OA_{1}=6,OA_{1}=2,AO=2OA_{1}=4.$
Ответ: 4.
Задача 3. Периметр треугольника равен 39. Найдите его стороны, если стороны подобного ему треугольника равны 3, 4 и 6.
Решение.
Пусть коэффициент подобия треугольников равен 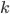$k$. Тогда искомые стороны равны $\displaystyle 3k,4k$ и $6k$. Периметр $\displaystyle P=3k+4k+6k=39;\; k=3.$ Найдём стороны: 9, 12 и 18.
Ответ: 9, 12, 18.