Для того чтобы решить задания, в которых требуется найти координаты точки пересечения графиков (заданных уравнениями), удовлетворяющей определённому условию, нужно
• составить и решить систему уравнений, задающих графики, тем самым найдя все их точки пересечения;
• определить условия, отличающие искомую точку от других (например, знак абсциссы), выбрать среди всех найденных точек пересечения искомую.
Пример 1. На рисунке 1 изображены графики функций 
и 
. Вычислите координаты точки 
.
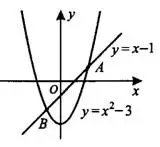
Рис.1
Решение.
Решим систему уравнений 
Таким образом, решениями системы являются точки 
и 
.
Точка расположена слева от оси 
, точка 
— справа, следовательно, абсцисса точки — отрицательное число, в то время как абсцисса точки — положительное. Среди найденных точек пересечения выбираем точку с отрицательной абсциссой: .
Ответ: .
Пример 2. На рисунке 2 изображены графики функций 
и 
. Вычислите координаты точки .
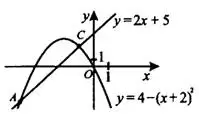
Рис.2
Решение.
а) Решим систему уравнений 
Таким образом, решениями системы являются точки 
и 
.
б) Точка расположена ниже оси 
, точка 
— выше, следовательно, ордината точки — отрицательное число, ордината точки — положительное.
в) Среди найденных точек пересечения выбираем точку с отрицательной ординатой: .
Ответ: .
Замечание. Можно было бы рассуждать иначе: точка левее точки , поэтому абсцисса точки меньше абсциссы точки . Из точек и абсцисса точки меньше, поэтому точка является искомой.
