Углы. Готовимся к ОГЭ по математике. Модуль 2. Урок 43

Фигура, образованная двумя лучами с общим началом, называется углом. Также углом называют и часть плоскости, ограниченную этими лучами.
Общее начало лучей называется вершиной угла, а сами лучи — сторонами угла (см. рис. 1).

Рис. 1

Изображённые на рисунке 1 углы обозначаются 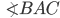$\displaystyle \angle BAC$ (или $\displaystyle \angle CAB$, или просто $\displaystyle \angle A$). Но обычно в геометрии рассматриваются «меньшие» углы (см. рис. 1 а), мы тоже будем следовать этому обозначению.
Угол называется развёрнутым, если его стороны вместе образуют прямую (см. рис. 2). Величина развёрнутого угла равна 180°.

Рис. 2

Два угла называются смежными, если одна сторона у них общая, а две другие составляют вместе прямую. Например, на рисунке 3 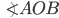$\displaystyle \angle AOB$ и $\displaystyle \angle BOC$ смежные. Сумма смежных углов равна 180° ($\displaystyle \angle COB+\angle BOA=180^{\circ}$).

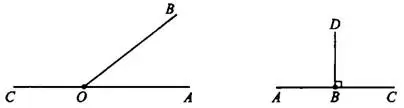
Рис. 3                                                    Рис. 4

Угол, равный своему смежному, называется прямым. Например, на рисунке 4 $\displaystyle \angle ABD$ и $\displaystyle \angle DBC$ прямые. Прямой угол равен 90°. $DB$ — перпендикуляр к прямой $AC$.
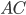Если мы из одной точки опустим перпендикуляр и наклонную к заданной прямой, то длина перпендикуляра будет меньше.
Биссектриса — это луч, исходящий из вершины угла и делящий его пополам. На рисунке 5 $BD$ — биссектриса угла $ABC$ ($\displaystyle \angle ABD=\angle DBC=\frac{1}{2}\angle ABC$).

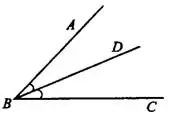
Рис. 5

Если угол меньше 90°, он называется острым, если больше 90°, но меньше 180° — тупым.
Две прямые при пересечении образуют 4 угла (см. рис. 6).

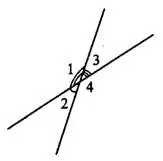
Рис. 6

Прямые, пересекающиеся под прямым углом, называются перпендикулярными (если прямые $a$ и $b$ перпендикулярны, пишут $\displaystyle a\perp b$).
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны. Например, на рисунке 7 $\displaystyle \angle AOB=\angle COD,\angle AOC=\angle BOD$.

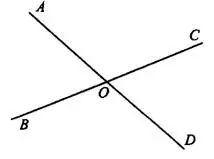
Рис. 7

В качестве угла между прямыми берётся тот угол, который не является тупым.
Задача 1. Найдите градусную меру угла $\displaystyle \angle COB$, если $\displaystyle \angle AOC=150^{\circ}$ (см. рис. 8).

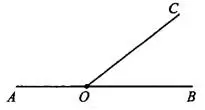
Рис. 8

Решение. $\displaystyle \angle AOC$ и $\displaystyle \angle COB$ - смежные, значит, $\displaystyle \angle AOC+\angle COB=180^{\circ},\; \angle COB=180^{\circ}-150^{\circ}=30^{\circ}$.
Ответ: 30.