Сумма углов треугольника равна 180°.
Сумма двух сторон треугольника больше третьей.
Против большей стороны треугольника лежит больший угол.
Против большего угла треугольника лежит его большая сторона.
Треугольник, у которого один угол тупой, называется тупоугольным.
Внешние углы треугольника
Угол, смежный с каким-нибудь углом треугольника, называется внешним углом треугольника. Например,  (см. рис.1) — внешний угол
(см. рис.1) — внешний угол  .
.
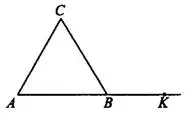
Рис.1
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним  , (см. рис.1).
, (см. рис.1).
Равенство треугольников
Равные треугольники — это такие треугольники, которые можно совместить друг с другом, наложив друг на друга так, чтобы они совпали.
Признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
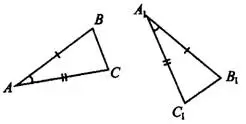
Рис.2
Например, если  (см. рис.2), то
(см. рис.2), то  .
.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
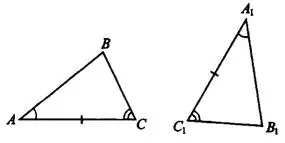
Рис.3
Например, если  и
и  , то
, то  (см. рис.3).
(см. рис.3).
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
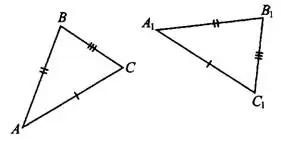
Рис.4
Например, если  , то
, то  (см. рис.4).
(см. рис.4).
Подобие фигур
Часто встречаются фигуры, которые имеют разные размеры, но одинаковую форму, например, все круги или все квадраты. Такие фигуры называют подобными.
Треугольники  и
и  подобны друг другу (
подобны друг другу ( ), если
), если  и
и  , где
, где  называют коэффициентом подобия (см. рис.5).
называют коэффициентом подобия (см. рис.5).
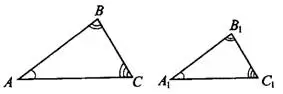
Рис.5
В подобных треугольниках медианы, биссектрисы, высоты и периметры пропорциональны с тем же коэффициентом. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Признаки подобия треугольников
1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Например, если  , то
, то  (см. рис.6).
(см. рис.6).
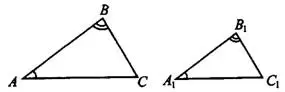
Рис.6
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими двумя сторонами, равны, то такие треугольники подобны.
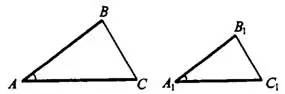
Рис.7
Например, если  и
и  , то
, то  (см. рис.7).
(см. рис.7).
3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то такие треугольники подобны.
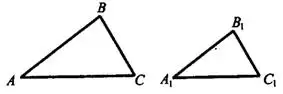
Рис.8
Например, если  , то
, то  (см. рис.8).
(см. рис.8).
Задача 1. Найдите градусную меру угла  треугольника
треугольника  (см. рис.9), если
(см. рис.9), если  .
.
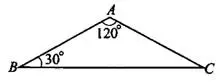
Рис.9
Решение.
 , откуда
, откуда  .
.
Ответ: 30.
Задача 2. Найдите градусную меру меньшего угла между биссектрисами углов  , проведёнными из вершин
, проведёнными из вершин  и
и  , если
, если  .
.
Решение.
Найдём угол  , используя теорему о сумме углов треугольника.
, используя теорему о сумме углов треугольника.
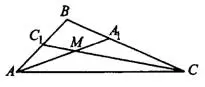
Рис.10
 .
.
 и
и  — биссектрисы (см. рис.10), поэтому
— биссектрисы (см. рис.10), поэтому  .
.
Меньший угол между биссектрисами — это внешний угол  .
.
Ответ: 35.
Задача 3. Найдите сторону  треугольника
треугольника  , если
, если
 (см. рис.11).
(см. рис.11).
Решение.
 по двум углам (первый признак подобия треугольников).
по двум углам (первый признак подобия треугольников).

Ответ: 5.
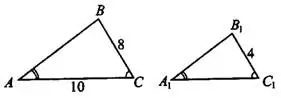
Рис.11







