Треугольник. Готовимся к ОГЭ по математике. Модуль 2. Урок 45

Рассмотрим три точки, не лежащие на одной прямой. Это - вершины треугольника. Соединим их отрезками — это будут стороны треугольника.
Треугольником называется многоугольник с тремя углами. Например, на рисунке 1 изображён $\displaystyle \bigtriangleup ABC$ (так обозначается треугольник с заданными вершинами).

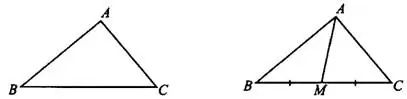
Рис.1                                                           Рис.2

Периметром треугольника называется сумма длин его сторон. Например, периметр $\displaystyle \bigtriangleup ABC$ (см. рис.1) равен $\displaystyle AB+BC+CA$.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Например, $AM$ — медиана $\displaystyle \bigtriangleup ABC$ (см. рис.2).
Биссектриса треугольника — отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противоположной стороны. Проще говоря, отрезок $AK$ — биссектриса треугольника $ABC$, если /.ВАК = ZСАК (см. рис.3).

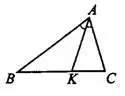
Рис.3

Высотой треугольника называется отрезок, соединяющий вершину треугольника с точкой противоположной стороны (или её продолжения) и перпендикулярный этой стороне. Например, 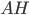$AH$ — высота $\displaystyle \bigtriangleup ABC$ (см. рис.4).

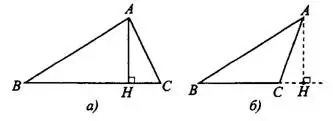
Рис.4

Задача 1. Укажите номера верных утверждений.
1) Сумма смежных углов равна 90°.
2) При пересечении параллельных прямых секущей накрест лежащие углы равны.
3) Вертикальные углы равны.
4) Если точки $\displaystyle A_{1},A_{2}$ лежат на одной стороне угла $\displaystyle \angle B_{2}OA_{2}$, а точки $\displaystyle B_{1},B_{2}$ — на другой, $\displaystyle A_{1}B_{1}\parallel A_{2}B_{2}$ и $\displaystyle OA_{1}=A_{1}A_{2}$, то $\displaystyle B_{1}B_{2}=2OB_{1}$ (см. рис.5).

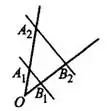
Рис.5

5) Развёрнутым называется угол, меньший 90°.
Решение.
Утверждение 1) неверно, так как сумма смежных углов равна 180°.
Утверждение 2) верно, так как оно является свойством параллельных прямых.
Утверждение 3) верно по свойству вертикальных углов.
Утверждение 4) неверно, так как $\displaystyle B_{1}B_{2}=OB_{1}$ по теореме Фалеса (см. рис.5).
Утверждение 5) неверно, так как развёрнутый угол равен 180°.
Ответ: 23.