Покажем решение неравенств методом интервалов.
Пример 1. Решите неравенство  .
.
Решение.
1) Разложим левую часть неравенства на множители. Для этого решим уравнение  .
.  и
и  — корни уравнения. Неравенство примет вид
— корни уравнения. Неравенство примет вид  .
.
2) Нанесём числа —3 и 7 на прямую. Учитывая, что неравенство нестрогое, закрасим точки (см. рис. 1).
![]()
3) Так как , то на крайнем правом промежутке поставим знак «+» (можно из любого промежутка взять число и подставить в левую часть неравенства, например, если  , получим ) (см. рис. 2).
, получим ) (см. рис. 2).
![]()
4) Так как множители  и
и  в нечётной степени (в первой), то на остальных промежутках знаки чередуем и рисуем «змейку» (см. рис. 3).
в нечётной степени (в первой), то на остальных промежутках знаки чередуем и рисуем «змейку» (см. рис. 3).

5) Левая часть неравенства больше или равна 0, значит, выделяем промежутки со знаком «+» (см. рис. 4).
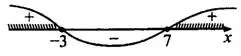
6) Делаем вывод:  .
.
Ответ: (—оо; —3] U [7; +оо).
Пример 2. Решите неравенство  .
.
Решение.
 ,
,  — корни уравнения.
— корни уравнения.


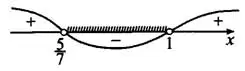
 (см. рис. 5).
(см. рис. 5).
Ответ:  .
.
Пример 3. Решите неравенство .
Решение.
Умножим обе части неравенства на (—1).
 ,
,  ,
, 
 — корни уравнения.
— корни уравнения.
 .
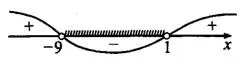
.  (см. рис. 6).
(см. рис. 6).
Ответ: (—9; 1).
Пример 4. Решите неравенство .
Решение.
Заметим, что левая часть неравенства — полный квадрат, то есть  . Неравенство примет вид , отсюда решение этого неравенства — любое число, кроме
. Неравенство примет вид , отсюда решение этого неравенства — любое число, кроме 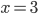 , так как неравенство строгое.
, так как неравенство строгое.
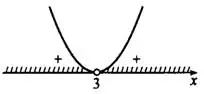
 и (см. рис. 7).
и (см. рис. 7).
Ответ:  .
.
Пример 3. Решите неравенство 
Решение.
Нули числителя:  . Нули знаменателя:
. Нули знаменателя:  .
.
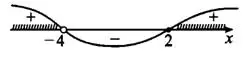
 (см. рис. 8).
(см. рис. 8).
Ответ: 







