Квадратное неравенство — это неравенство вида 

 где
где  — переменная,
— переменная,  и
и  — некоторые числа, причём
— некоторые числа, причём 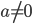 .
Покажем решение квадратных неравенств на примерах.
.
Покажем решение квадратных неравенств на примерах.
Пример 1. Решите неравенство .
Решение.
1. Решим уравнение  .
.



2. Графиком функции  является парабола, ветви которой направлены вверх (). Парабола пересекает ось
является парабола, ветви которой направлены вверх (). Парабола пересекает ось  в двух точках, абсциссы которых 0,5 и —6 (см. рис. 1).
в двух точках, абсциссы которых 0,5 и —6 (см. рис. 1).
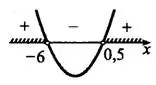
3. Вывод: данное неравенство выполняется, если  и .
и .
Ответ:  .
.
Покажем, как можно записывать решение квадратного неравенства, если вид графика анализировать устно.
Пример 2. Решите неравенство  .
.
Решение.
Решим уравнение  .
.

По теореме, обратной теореме Виета, имеем 
Следовательно, 
Вывод: данное неравенство выполняется, если  (см. рис. 2).
(см. рис. 2). 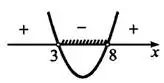
Ответ: (3;8).
Пример 3. Решите неравенство  . В ответе укажите наибольшее целое решение неравенства.
. В ответе укажите наибольшее целое решение неравенства.
Решение.
Решим уравнение  .
.



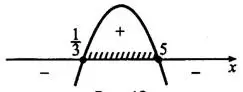
 (см. рис. 3). Наибольшее целое решение неравенства равно 5.
(см. рис. 3). Наибольшее целое решение неравенства равно 5.
Ответ: 5.
Пример 4. Решите неравенство .
Решение.
Решим уравнение  .
.

 Уравнение
Уравнение  корней не имеет, значит, график функции
корней не имеет, значит, график функции  не пересекает ось
не пересекает ось  (см. рис. 4).
(см. рис. 4). 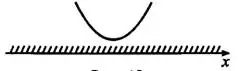
Учитывая, что , неравенство выполняется при любом значении  .
.
Ответ:  .
.
Заметим, что если коэффициент при  отрицательный (
отрицательный (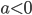 ), то обе части неравенства можно умножить на (-1), изменив знак неравенства на противоположный, и тогда ветви параболы будут направлены вверх.
), то обе части неравенства можно умножить на (-1), изменив знак неравенства на противоположный, и тогда ветви параболы будут направлены вверх.
Пример 5. Решите неравенство  .
.
Решение.


Решим уравнение 



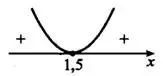
Учитывая, что , неравенство  выполняется только при
выполняется только при  (см. рис. 5).
(см. рис. 5).
Ответ: 1,5.







