Задача 7. Периметр прямоугольной трапеции, описанной около окружности, равен 42, её большая боковая сторона равна 12 (см. рис. 8). Найдите радиус окружности.
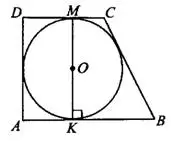
Решение.
У четырёхугольника, описанного около окружности, суммы длин противоположных сторон равны, то есть
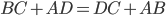 . Поэтому
. Поэтому 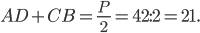
Наибольшая боковая сторона 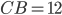 , отсюда
, отсюда 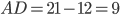 . Так как
. Так как  , то
, то 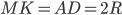 , где
, где 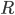 — радиус вписанной окружности. Тогда
— радиус вписанной окружности. Тогда 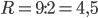 .
.
Ответ: 4,5.
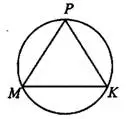
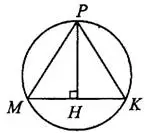
Задача 8. Боковые стороны равнобедренного треугольника равны 30, основание равно 36 (см. рис. 9). Найдите радиус описанной окружности этого треугольника.
Решение.
По теореме синусов 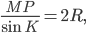 где
где 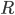 — радиус описанной около
— радиус описанной около 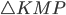 окружности. Пусть
окружности. Пусть 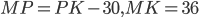 . Проведём высоту
. Проведём высоту 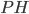 (см. рис. 10). В равнобедренном треугольнике
(см. рис. 10). В равнобедренном треугольнике 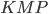 высота
высота 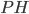 является медианой,
является медианой, 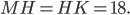 Найдём
Найдём 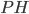 по теореме Пифагора.
по теореме Пифагора.
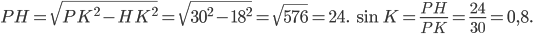
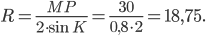
Ответ: 18,75.
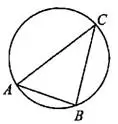
Задача 9. Угол  треугольника
треугольника  , вписанного в окружность радиусом 12, равен 30° (см. рис. 11). Найдите сторону
, вписанного в окружность радиусом 12, равен 30° (см. рис. 11). Найдите сторону  этого треугольника.
этого треугольника.
Решение.
По теореме синусов для радиуса описанной окружности 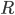 выполняется
выполняется 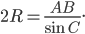
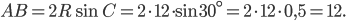
Ответ: 12.
Задача 10. Радиус окружности, описанной около прямоугольного треугольника, равен 14. Найдите гипотенузу этого треугольника.
Решение.
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, значит, гипотенуза — диаметр. Тогда гипотенуза равна 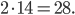
Ответ: 28.
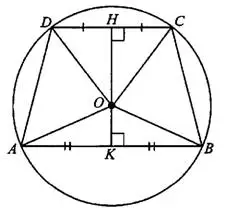
Задача 11. Основания равнобедренной трапеции равны 18 и 80. Радиус описанной окружности равен 41 (см. рис. 12). Найдите высоту трапеции, если центр описанной окружности лежит внутри трапеции.
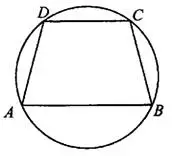
Решение.
Проведём высоту 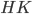 через центр окружности
через центр окружности 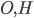 и
и 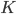 будут лежать на серединах оснований (см. рис. 13).
будут лежать на серединах оснований (см. рис. 13). 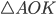 и
и 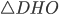 — прямоугольные,
— прямоугольные, 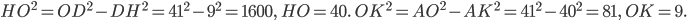
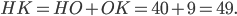
Ответ: 49.







