Описанные и вписанные окружности (задачи). Готовимся к ЕГЭ по математике. Геометрия. Урок 19

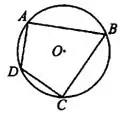
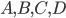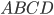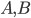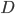Задача 12. Точки $A, B, C, D$ , расположенные на окружности, являются вершинами четырёхугольника $ABCD$ . Градусные величины углов $A, B$ и $D$ относятся соответственно как 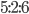$5:2:6$ (см. рис. 14). Найдите угол С четырёхугольника $ABCD$ . Ответ дайте в градусах.

Рис. 14.

Решение.
Четырёхугольник $ABCD$ — вписанный, поэтому сумма его противоположных углов равна 180°.
По условию, 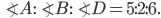$\displaystyle \angle A:\angle B:\angle D=5:2:6.$
Обозначим $\displaystyle \angle A=5x,\; \angle B=2x,\; \angle D=6x.$
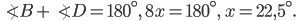
$\displaystyle \angle B+ \angle D=180^{\circ},\; 8x=180^{\circ},\; x=22,5^{\circ}.$
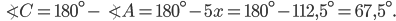
$\displaystyle \angle C=180^{\circ}-\angle A=180^{\circ}-5x=180^{\circ}-112,5^{\circ}=67,5^{\circ}.$
Ответ: 67,5.
Задача 13. Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 7 (см. рис. 15).

Рис. 15.

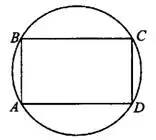
Решение.
Если прямоугольник вписан в окружность, то центр этой окружности лежит на середине его диагонали, то есть диагональ в 2 раза больше радиуса. 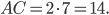$\displaystyle AC=2\cdot 7=14.$
Ответ: 14.
Задача 14. Периметр правильного шестиугольника равен 612 (см. рис. 16). Найдите диаметр описанной окружности.
Решение.

Рис. 16.

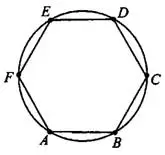
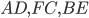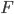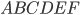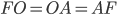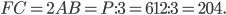
Проведём диагонали $AD, FC, BE$ (см. рис. 17). В правильном шестиугольнике все стороны и углы равны, а диаметр описанной окружности проходит через противоположные вершины, например $F$ и $C$ . Треугольники, на которые разбился $ABCDEF$ , правильные, то есть $FO = OA = AF$ . Диаметр $FC$ в 2 раза больше стороны шестиугольника, $FC = 2AB = P : 3 = 612 : 3 = 204.$

Рис. 17.

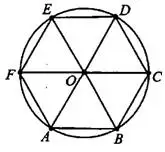
Ответ: 204.
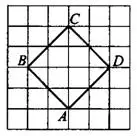
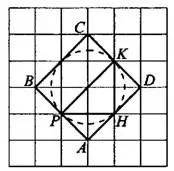
Задача 15. Найдите радиус окружности, вписанной в квадрат 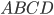$ABCD$ (см. рис. 18), считая стороны квадратных клеток равными 1. В ответе укажите значение радиуса, умноженное на $\displaystyle \sqrt{2}$ .

Рис. 18.

Решение.
Построим окружность (см. рис. 19).
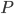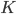Так как квадрат — фигура симметричная, точки касания $P$ и $K$ являются серединами его сторон. Видно, что радиус равен половине 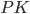$PK$ . Найдём 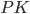$PK$ по теореме Пифагора из прямоугольного треугольника $PKH$ .

Рис. 19.

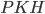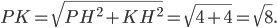$\displaystyle PK=\sqrt{PH^{2}+KH^{2}}=\sqrt{4+4}=\sqrt{8}.$ Радиус равен 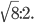$\displaystyle \sqrt{8}:2.$ Значение радиуса, умноженное на 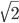$\displaystyle \sqrt{2}$ , равно
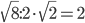$\displaystyle \sqrt{8}:2\cdot \sqrt{2}=2$ .
Ответ: 2.
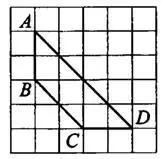
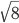Задача 16. Найдите среднюю линию трапеции $ABCD$ (см. рис. 20), если стороны клеток равны $\displaystyle \sqrt{8}$ .

Рис. 20.

Решение.
Средняя линия трапеции соединяет середины боковых сторон трапеции (см. рис. 21).

Рис. 21.

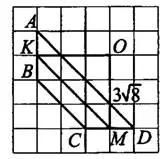
Назовём её 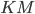$KM$ и найдём из прямоугольного треугольника 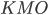$KMO$ . Длина трёх клеток равна 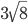$\displaystyle 3\sqrt{8}$ . Тогда
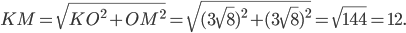
$\displaystyle KM=\sqrt{KO^{2}+OM^{2}}=\sqrt{(3\sqrt{8})^{2}+(3\sqrt{8})^{2}}=\sqrt{144}=12.$
Ответ: 12.