Рассмотрим прямоугольный треугольник  , в котором угол
, в котором угол  равен 90°.
равен 90°.

Стороны 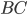 и
и 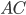 называются катетами, сторона
называются катетами, сторона  называется гипотенузой. Для угла
называется гипотенузой. Для угла  прилежащий катет
прилежащий катет 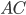 (лежит на стороне угла), противолежащий катет
(лежит на стороне угла), противолежащий катет 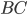 .
.
Для прямоугольного треугольника выполняется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов: 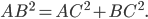
Например, 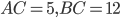 . Найдём
. Найдём  .
.
В нашем треугольнике  — гипотенуза,
— гипотенуза, 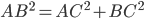 ,
, 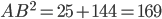 ,
, 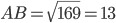 . Теперь разберём случай, когда нужно найти катет. Пусть
. Теперь разберём случай, когда нужно найти катет. Пусть 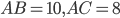 . Найдём
. Найдём 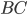 .
.
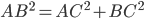 , отсюда
, отсюда 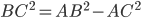 ,
, 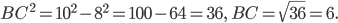
Теперь вспомним определения синуса, косинуса и тангенса острого угла прямоугольного треугольника.
Синусом угла называют отношение противолежащего катета к гипотенузе. Для нашего треугольника 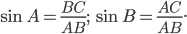
Косинусом угла называют отношение прилежащего катета к гипотенузе. Для нашего треугольника 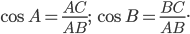
Обратите внимание, в одном и том же прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла, т.е. 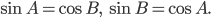
Тангенсом угла называют отношение противолежащего катета к прилежащему. Для нашего треугольника 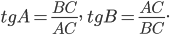
Видно, что 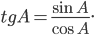
Основное тригонометрическое тождество позволяет найти синус угла, если известен косинус этого угла, и наоборот.
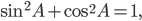 или для острого угла
или для острого угла 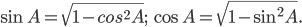
Задача 1. В треугольнике  угол
угол  равен 90°,
равен 90°,  = 20,
= 20, 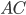 = 16. Найдите
= 16. Найдите 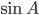 .
.
Решение.
Синусом угла называют отношение противолежащего катета к гипотенузе. По теореме Пифагора, 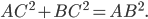 найдём противолежащий углу
найдём противолежащий углу  катет
катет 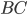 (см. рис. 1).
(см. рис. 1).
 ,
, 
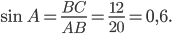
Ответ: 0,6.
Задача 2. В треугольнике  угол
угол  равен 90°,
равен 90°, 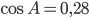 . Найдите
. Найдите 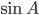 .
.
Решение.
Так как угол  - острый, то
- острый, то 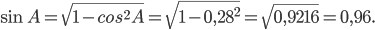
Ответ: 0,96.
Задача 3. В треугольнике  угол
угол  равен 90°,
равен 90°, 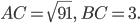 Найдите
Найдите  .
.
Решение.
Косинусом угла называют отношение прилежащего катета к гипотенузе. По теореме Пифагора найдём гипотенузу  (см. рис. 2).
(см. рис. 2). 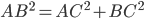 , отсюда
, отсюда 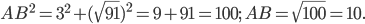
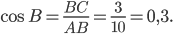
Ответ: 0,3.
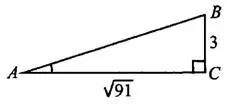
Задача 4. В треугольнике  угол
угол  равен 90°,
равен 90°, 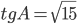 . Найдите
. Найдите  .
.
Решение.
Тангенсом угла называют отношение противолежащего катета к прилежащему. Так как треугольник  прямоугольный, угол
прямоугольный, угол  острый, то для нашего треугольника
острый, то для нашего треугольника
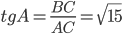 и можно считать, что
и можно считать, что 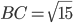 ,
,
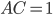 . По теореме Пифагора найдём гипотенузу
. По теореме Пифагора найдём гипотенузу  .
. 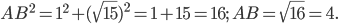
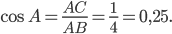
Ответ: 0,25.







