В прямоугольном параллелепипеде  стороны оснований
стороны оснований  и
и 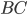 равны соответственно 8 и 5, а боковое ребро
равны соответственно 8 и 5, а боковое ребро  равно 4. На ребре
равно 4. На ребре  отмечена точка
отмечена точка 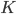 , а на луче
, а на луче 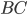 — точка
— точка 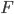 , причём
, причём  и
и  . Плоскость
. Плоскость  пересекает ребро
пересекает ребро  в точке
в точке 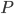 .
.
а) Докажите, что  .
.
б) Найдите площадь сечения параллелепипеда плоскостью  .
.
Решение.
а) Построим сечение параллелепипеда плоскостью  (см. рис. 1).
(см. рис. 1).
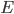 — точка пересечения ребра
— точка пересечения ребра  и отрезка
и отрезка  .
.
В плоскости  проведём лучи
проведём лучи  и
и  ,
,  пересекает
пересекает  в точке
в точке  . В плоскости
. В плоскости  проведём отрезок
проведём отрезок  ,
,  пересекает
пересекает  в точке
в точке 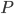 , а
, а  — в точке
— в точке 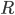 . Пятиугольник
. Пятиугольник  — искомое сечение.
— искомое сечение.
 , значит,
, значит,  — средняя линия
— средняя линия  , отсюда
, отсюда  , а так как
, а так как  , то
, то  — средняя линия
— средняя линия  ,
,
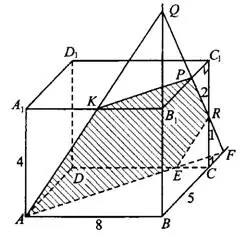
Рис.1

следовательно, 
б) Прямоугольные треугольники  и
и  равны по двум катетам
равны по двум катетам  , отсюда
, отсюда 
 как площадь равностороннего треугольника со стороной
как площадь равностороннего треугольника со стороной  .
. 

 по первому признаку подобия (
по первому признаку подобия ( ,
,  - как вертикальные). Из подобия следует,
- как вертикальные). Из подобия следует,  . По доказанному в а),
. По доказанному в а),  , тогда
, тогда  и
и  . Так как
. Так как  - средняя линия
- средняя линия  , то
, то 
В равнобедренном прямоугольном треугольнике 
 , тогда
, тогда  .
.
В  , отсюда
, отсюда
 — равносторонний.
— равносторонний. 

Ответ: 






