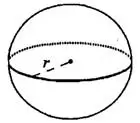
Шар
Рис. 1.
Объём шара и площадь его поверхности вычисляются по формулам
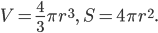
Задача 1. Объём шара равен  . Найдите площадь его поверхности, делённую на
. Найдите площадь его поверхности, делённую на 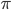 .
.
Решение.
Обозначим через 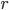 радиус шара. Тогда
радиус шара. Тогда 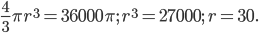 Площадь поверхности шара равна
Площадь поверхности шара равна 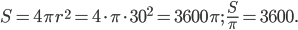
Ответ: 3600.
Задача 2. Площадь большого круга шара равна 10 (см. рис. 2). Найдите площадь поверхности шара.
Рис. 2.
Решение.
Обозначим радиус шара через 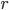 . Тогда площадь большого круга шара равна
. Тогда площадь большого круга шара равна 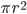 , а площадь поверхности шара —
, а площадь поверхности шара — 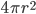 . Таким образом, площадь поверхности шара в 4 раза больше площади большого круга шара и равна
. Таким образом, площадь поверхности шара в 4 раза больше площади большого круга шара и равна 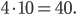
Ответ: 40.