Конус. Готовимся к ЕГЭ по математике. Геометрия. Урок 29

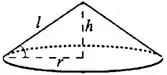
Объём конуса (см. рис. 1) может быть вычислен по той же формуле, что и объём пирамиды:

$$\displaystyle V=\frac{1}{3}S_{OCH}h.$$

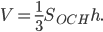
Если известен радиус основания 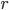$r$, то объём можно найти по формуле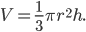

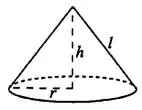
$$\displaystyle V=\frac{1}{3}\pi r^{2}h.$$

Площади боковой и полной поверхности конуса вычисляются следующим образом (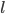$l$ — образующая):
$\displaystyle S_{bok}=\pi rl,\; S_{\Pi O\Lambda H}=\pi r(r+l).$

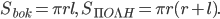
Задача 1. Найдите объём 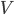$V$ конуса, образующая которого равна 10 и наклонена к плоскости основания под углом 30°. В ответе укажите $\displaystyle \frac{V}{\pi }$.
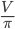Решение.
По условию, 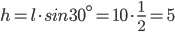$\displaystyle h=l\cdot sin30^{\circ}=10\cdot \frac{1}{2}=5$ (см. рис. 2); 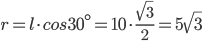$\displaystyle r=l\cdot cos30^{\circ}=10\cdot \frac{\sqrt{3}}{2}=5\sqrt{3}$. Искомый объём равен
$\displaystyle V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi \cdot (5\sqrt{3})^{2}\cdot 5=125\pi ;\; \frac{V}{\pi }=125.$
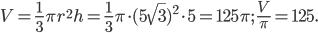
Ответ: 125.

Задача 2. Длина окружности основания конуса равна 4, образующая равна 5. Найдите площадь боковой поверхности конуса.
Решение.
Обозначим через 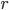$r$ радиус основания конуса, через 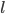$l$ образующую. Тогда по условию,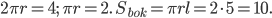 $\displaystyle 2\pi r=4;\; \pi r=2.\; S_{bok}=\pi rl=2\cdot 5=10.$
Ответ: 10.

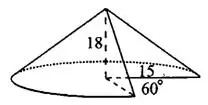
Задача 3. Найдите объём 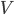$V$ части конуса, изображённой на рисунке 3. В ответе укажите $\displaystyle \frac{V}{\pi }$.

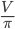Решение.
Угол 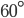$\displaystyle 60^{\circ}$, вырезанный из основания, составляет 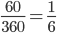$\displaystyle \frac{60}{360}=\frac{1}{6}$ часть полного угла. Таким образом, 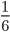$\displaystyle \frac{1}{6}$ часть конуса была удалена, 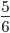$\displaystyle \frac{5}{6}$ осталось. Объём конуса с радиусом основания 15 и высотой 18 равен 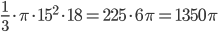$\displaystyle \frac{1}{3}\cdot \pi \cdot 15^{2}\cdot 18=225\cdot 6\pi =1350\pi$. Искомый объём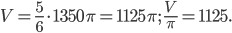 $\displaystyle V=\frac{5}{6}\cdot 1350\pi =1125\pi ;\; \frac{V}{\pi }=1125.$
Ответ: 1125.