Для объёма и площади боковой поверхности цилиндра (см. рис. 1) справедливы те же формулы, что и для призмы:
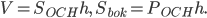
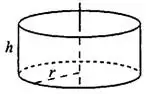
Рис. 1.
Если радиус основания равен 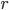 , то площадь основания цилиндра равна
, то площадь основания цилиндра равна 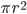 , а периметр —
, а периметр — 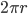 . Тогда формулы объёма цилиндра, площадей боковой и полной поверхности цилиндра имеют вид
. Тогда формулы объёма цилиндра, площадей боковой и полной поверхности цилиндра имеют вид
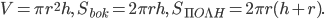
Задача 1. В цилиндрическом сосуде уровень жидкости достигает 45 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение.
Объём воды после переливания остаётся тем же:
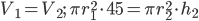 . Так как диаметр второго сосуда в 3 раза больше диаметра первого, то и радиус второго втрое больше радиуса первого:
. Так как диаметр второго сосуда в 3 раза больше диаметра первого, то и радиус второго втрое больше радиуса первого: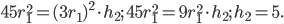
Ответ: 5.
Задача 2. Площадь осевого сечения цилиндра равна б (см. рис. 2). Найдите площадь боковой поверхности цилиндра, делённую на
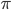 .
.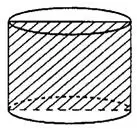
Рис. 2.
Решение.
Осевое сечение — это прямоугольник со сторонами 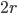 и
и 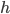 , где
, где 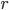 — радиус основания,
— радиус основания, 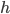 — высота цилиндра. Площадь этого прямоугольника равна
— высота цилиндра. Площадь этого прямоугольника равна 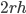 . Площадь боковой поверхности цилиндра равна
. Площадь боковой поверхности цилиндра равна 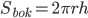 . Отсюда
. Отсюда 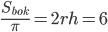 .
.
Ответ: б.







