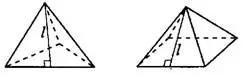
Объём тетраэдра и пирамиды (см. рис. 1) можно найти по формуле
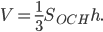
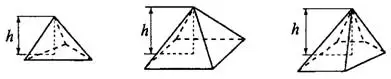
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания и апофемы (высоты боковой грани, проведённой из вершины пирамиды, см. рис. 2):
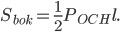
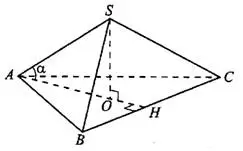
Высота правильной пирамиды падает в центр её основания. Углом между ребром и плоскостью основания называют угол между этим ребром и его проекцией на плоскость основания. На рисунке 3 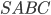 — правильная пирамида,
— правильная пирамида,
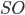 — высота. Тогда
— высота. Тогда  — центр основания
— центр основания  . Угол между ребром
. Угол между ребром 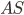 и плоскостью основания
и плоскостью основания 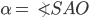 .
.
Углом между боковой гранью и плоскостью основания называют угол между апофемой боковой грани и проекцией этой апофемы на плоскость основания. На рисунке 4  — правильная пирамида,
— правильная пирамида, 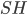 — апофема,
— апофема, 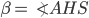 — угол между гранью
— угол между гранью 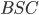 и плоскостью основания
и плоскостью основания  .
.
Задача 1. Стороны основания правильной четырёхугольной пирамиды (см. рис. 5) равны 16, боковые рёбра равны 17. Найдите площадь поверхности этой пирамиды.
Решение.
Проведём апофему 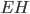 (см. рис. 6).
(см. рис. 6). 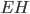 — высота равнобедренного треугольника
— высота равнобедренного треугольника 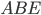 , поэтому является его медианой, и
, поэтому является его медианой, и 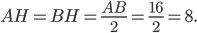
По теореме Пифагора для прямоугольного треугольника 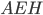 имеем
имеем 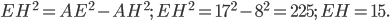 В основании пирамиды лежит квадрат с периметром
В основании пирамиды лежит квадрат с периметром 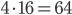 и площадью
и площадью 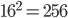 . Искомая площадь равна сумме площади основания и площади боковой поверхности:
. Искомая площадь равна сумме площади основания и площади боковой поверхности:
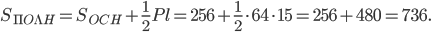
Ответ: 736.
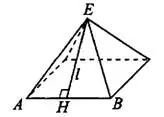
Задача 2. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60° (см. рис. 7). Высота пирамиды равна 12. Найдите объём пирамиды.
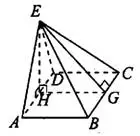
Решение.
По условию, высота пирамиды 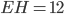 . Из прямоугольного треугольника
. Из прямоугольного треугольника 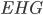 имеем
имеем 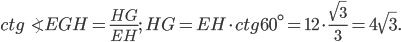
Аналогично из прямоугольного треугольника 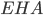 получаем
получаем 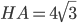 . Площадь прямоугольника в основании
. Площадь прямоугольника в основании
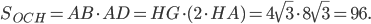
Объём пирамиды
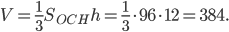
Ответ: 384.







