Параллелепипед и призма. Готовимся к ЕГЭ по математике. Геометрия. Урок 26

Параллелепипед и призма

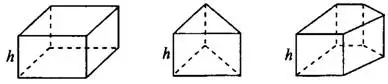
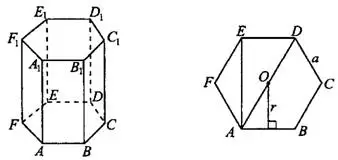
Объём параллелепипеда и призмы (см. рис. 1) может быть найден как произведение площади основания на высоту:

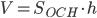
$\displaystyle V=S_{OCH}\cdot h$

Рис. 1.

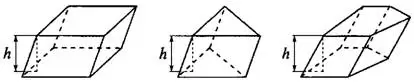
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту:

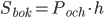
$\displaystyle S_{bok}=P_{och}\cdot h$

Площадь всей поверхности призмы равна сумме площади боковой поверхности и удвоенной площади основания (так как площади обоих оснований одинаковы):

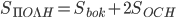
$\displaystyle S_{\Pi O\Lambda H}=S_{bok}+2S_{OCH}$

Если призма прямая (см. рис. 2), то формулы остаются прежними, но высота прямой призмы равна её боковому ребру. Напомним, что в прямой призме боковые рёбра перпендикулярны плоскости основания. В частности, любая правильная призма является прямой (но в основании правильной призмы к тому же обязательно лежит правильный многоугольник).

Рис. 2.

В правильной шестиугольной призме основание является правильным шестиугольником. Обозначив сторону этого шестиугольника через $a$ , получаем следующие соотношения (см. рис. 3):
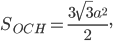
$\displaystyle S_{OCH}=\frac{3\sqrt{3}a^{2}}{2},$
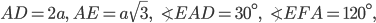
$\displaystyle AD=2a,\; AE=a\sqrt{3},\; \angle EAD=30^{\circ},\; \angle EFA=120^{\circ},$
радиус описанной окружности 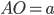$\displaystyle AO=a$ ,
радиус вписанной окружности 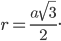$\displaystyle r=\frac{a\sqrt{3}}{2}.$

Рис. 3.

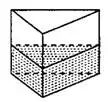
Задача 1. В сосуд, имеющий форму правильной треугольной призмы, налили 600 см³ воды (см. рис. 4) и полностью погрузили в неё деталь. При этом уровень жидкости в сосуде поднялся с отметки 12 см до отметки 16 см. Чему равен объём детали? Ответ выразите в см³.

Рис. 4.

Решение.
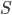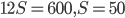Обозначим через $S$ площадь основания призмы. Тогда из формулы объёма призмы $\displaystyle V=Sh$ имеем $\displaystyle 12S=600, S=50$ (см²). После погружения детали суммарный объём детали и воды вычисляется по той же формуле: 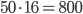$\displaystyle 50\cdot 16=800$ (см³). Объём детали равен $\displaystyle 800-600=200$ (см³).
Ответ: 200.
Задача 2. Через среднюю линию основания треугольной призмы, объём которой равен 48, проведена плоскость, параллельная боковому ребру (см. рис. 5). Найдите объём отсечённой треугольной призмы.

Рис. 5.

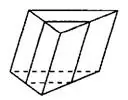
Решение.
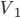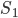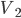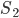Обозначим через $\displaystyle V_{1}$ и $\displaystyle S_{1}$ объём и площадь основания исходной призмы, через $\displaystyle V_{2}$ и $\displaystyle S_{2}$ объём и площадь основания отсечённой призмы. Так как у обеих призм общая высота, то 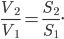$\displaystyle \frac{V_{2}}{V_{1}}=\frac{S_{2}}{S_{1}}.$ Средняя линия отсекает от треугольника в основании исходной призмы подобный треугольник, коэффициент подобия 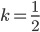$\displaystyle k=\frac{1}{2}$ (так как средняя линия в 2 раза меньше параллельной ей стороны треугольника). Отсюда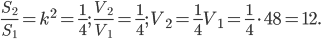 $\displaystyle \frac{S_{2}}{S_{1}}=k^{2}=\frac{1}{4};\; \frac{V_{2}}{V_{1}}=\frac{1}{4};\; V_{2}=\frac{1}{4}V_{1}=\frac{1}{4}\cdot 48=12.$
Ответ: 12.
Задача 3. Основанием прямой треугольной призмы (см. рис. 6) служит прямоугольный треугольник с катетами 5 и 12. Площадь её поверхности равна 180. Найдите высоту призмы.

Рис. 6.

Решение.
По теореме Пифагора можно найти гипотенузу с треугольника в основании призмы, 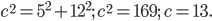$\displaystyle c^{2}=5^{2}+12^{2};\; c^{2}=169;\; c=13.$ Периметр основания призмы равен 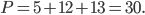$\displaystyle P=5+12+13=30.$ Площадь прямоугольного треугольника в основании равна половине произведения его катетов: 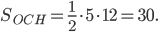$\displaystyle S_{OCH}=\frac{1}{2}\cdot 5\cdot 12=30.$ Площадь боковой поверхности равна 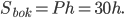$\displaystyle S_{bok}=Ph=30h.$ В условии дана площадь всей поверхности призмы 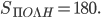$\displaystyle S_{\Pi O\Lambda H}=180.$ Отсюда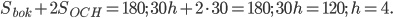 $\displaystyle S_{bok}+2S_{OCH}=180;\; 30h+2\cdot 30=180;\; 30h=120;\; h=4.$
Ответ: 4.