Соотношения в прямоугольном параллелепипеде и кубе. Готовимся к ЕГЭ по математике. Геометрия. Урок 25

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 5. Площадь поверхности этого параллелепипеда равна 62. Найдите третье ребро, выходящее из той же вершины.
Решение.
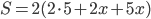Нам известны два измерения прямоугольного параллелепипеда (2 и 5), нужно найти третье измерение. Обозначим его через $x$. Тогда площадь поверхности параллелепипеда равна $\displaystyle S=2(2\cdot 5+2x+5x)$. По условию 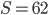$\displaystyle S=62$, поэтому 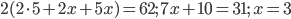$\displaystyle 2(2\cdot 5+2x+5x)=62;\; 7x+10=31;\; x=3$. Искомое ребро равно 3.
Ответ: 3.
Задача 2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объём этого параллелепипеда равен 36. Найдите диагональ параллелепипеда.
Решение.
Если обозначить неизвестное ребро через а, то объём равен 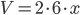$\displaystyle V=2\cdot 6\cdot x$. По условию 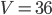$\displaystyle V=36$, поэтому 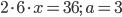$\displaystyle 2\cdot 6\cdot x=36;\; a=3$. Найдём диагональ данного прямоугольного параллелепипеда.
$\displaystyle d^{2}=2^{2}+6^{2}+3^{2};\; d^{2}=4+36+9;\; d^{2}=49;\; d=7.$
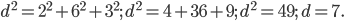
Ответ: 7.
Задача 3. Если каждое ребро куба увеличить на 1, то площадь его поверхности увеличится на 90. Найдите ребро куба.
Решение.
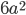Обозначим ребро куба через $a$. Тогда площадь поверхности исходного куба равна $\displaystyle 6a^{2}$, а площадь поверхности увеличенного куба 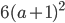$\displaystyle 6(a+1)^{2}$. По условию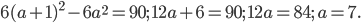 $\displaystyle 6(a+1)^{2}-6a^{2}=90;\; 12a+6=90;\; 12a=84;\; a=7.$
Ответ: 7.