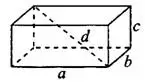
Прямоугольный параллелепипед. Готовимся к ЕГЭ по математике. Геометрия. Урок 24

Прямоугольный параллелепипед

Рис. 1.

Объём прямоугольного параллелепипеда («кирпича», см. рис. 1) равен произведению трёх его измерений:

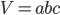$\displaystyle V=abc$ .

Площадь поверхности прямоугольного параллелепипеда равна сумме площадей его шести граней:

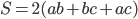$\displaystyle S=2(ab+bc+ac)$ .

Диагональю прямоугольного параллелепипеда называют отрезок, соединяющий его противоположные вершины. Квадрат длины этого отрезка равен сумме квадратов трёх измерений параллелепипеда:

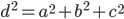$\displaystyle d^{2}=a^{2}+b^{2}+c^{2}$ .

Если все три измерения прямоугольного параллелепипеда равны, то такой параллелепипед называется кубом (см. рис. 2).

Рис. 2.

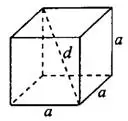
Для куба формулы объёма, площади и длины диагонали имеют вид

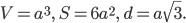
$\displaystyle V=a^{3},\; S=6a^{2},\; d=a\sqrt{3}.$

Разбиение тела на прямоугольные параллелепипеды

В следующих задачах требуется найти объём или площадь поверхности многогранника с прямыми двугранными углами. При решении сначала разбивают данный многогранник на несколько прямоугольных параллелепипедов, а затем подсчитывают объём или площадь поверхности каждого параллелепипеда в отдельности.
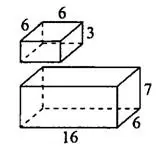
Задача 1. Найдите объём многогранника, изображённого на рисунке 3 (все двугранные углы многогранника прямые).

Рис. 3.

Решение.

Рис. 4.

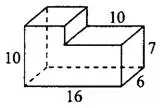
Данный многогранник составлен из двух прямоугольных параллелепипедов (см. рис. 4). Измерения большого параллелепипеда равны 16, 6 и 7. Измерения малого параллелепипеда равны 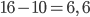$16 - 10 = 6,\; 6$ и $10 - 7 = 3.$
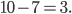
Суммарный объём этих параллелепипедов равен 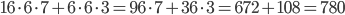$16 \cdot 6 \cdot 7 + 6 \cdot 6 \cdot 3 = 96 \cdot 7 + 36 \cdot 3 = 672 + 108 = 780$ .
Ответ: 780.
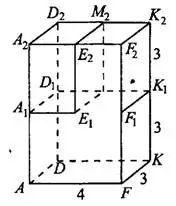
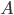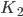Задача 2. Найдите квадрат расстояния между вершинами $\displaystyle A$ и $\displaystyle K_{2}$ многогранника, изображённого на рисунке 5. Все двугранные углы многогранника прямые.

Рис. 5.

Решение.

Рис. 6.

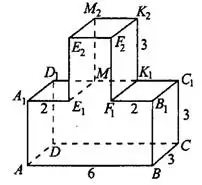
Проведём плоскость 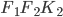$\displaystyle F_{1}F_{2}K_{2}$ и отбросим ту часть фигуры, которая оказалась справа. Достроим оставшуюся часть многогранника до прямоугольного параллелепипеда 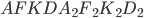$\displaystyle AFKDA_{2}F_{2}K_{2}D_{2}$ (см. рис. 6). Квадрат диагонали 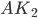$\displaystyle AK_{2}$ найдём по формуле
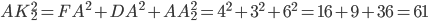$\displaystyle AK_{2}^{2}=FA^{2}+DA^{2}+AA_{2}^{2}=4^{2}+3^{2}+6^{2}=16+9+36=61$ .
Ответ: 61.
Задача 3. Найдите тангенс угла 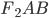$\displaystyle F_{2}AB$ многогранника, изображённого на рисунке 7. Все двугранные углы многогранника прямые.

Рис. 7.

Решение.

Рис. 8.

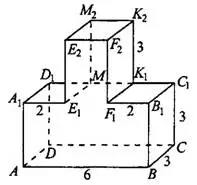
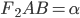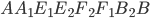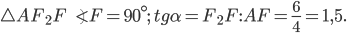
Заметим, что угол $\displaystyle F_{2}AB=\alpha$ лежит в плоскости грани $\displaystyle AA_{1}E_{1}E_{2}F_{2}F_{1}B_{2}B$ многогранника (см. рис. 8). Все углы многогранника прямые, поэтому $\displaystyle F_{2}F_{1}\perp AB$ . В прямоугольном $\displaystyle \bigtriangleup AF_{2}F\; \angle F=90^{\circ};\; tg\alpha =F_{2}F:AF=\frac{6}{4}=1,5.$
Ответ: 1,5.
Задача 4. Найдите площадь поверхности многогранника, изображённого на рисунке 9 (все двугранные углы прямые).

Рис. 9.

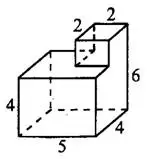
Решение.
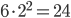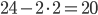Данный многогранник составлен из куба с ребром 2 и параллелепипеда 5x4x4. Площадь поверхности куба равна $\displaystyle 6\cdot 2^{2}=24$ . Учтём, что нижняя грань куба «склеена» с параллелепипедом, поэтому её площадь не включается в площадь исходного многогранника. Остаётся $\displaystyle 24-2\cdot 2=20$ .
Площадь поверхности параллелепипеда равна 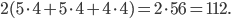$\displaystyle 2(5\cdot 4+5\cdot 4+4\cdot 4)=2\cdot 56=112.$ Также следует учесть, что квадрат 2x2 верхней грани параллелепипеда не будет включён в конечную площадь. Остаётся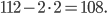 $\displaystyle 112-2\cdot 2=108.$
Искомая площадь равна 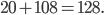$20 + 108 = 128.$
Ответ: 128.
Задача 5. Найдите площадь поверхности многогранника, изображённого на рисунке 10 (все двугранные углы прямые).

Рис. 10.

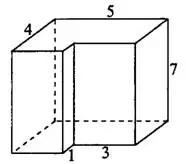
Решение.
При решении этой задачи данный многогранник удобнее всего рассматривать как прямую призму с высотой 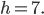$h = 7.$ Основанием этой призмы является многоугольник (см. рис. 11) с периметром 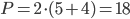$\displaystyle P=2\cdot (5+4)=18$ и площадью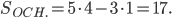 $\displaystyle S_{OCH.}=5\cdot 4-3\cdot 1=17.$

Рис. 11.

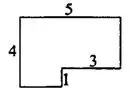
Тогда площадь боковой поверхности призмы равна 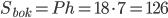$\displaystyle S_{bok}=Ph=18\cdot 7=126$ , а площадь всей поверхности равна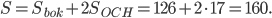 $\displaystyle S=S_{bok}+2S_{OCH}=126+2\cdot 17=160.$
Ответ: 160.