Уравнение — это равенство, содержащее неизвестную, значение которой надо найти.
Корень уравнения — это значение неизвестной, при котором данное уравнение обращается в верное равенство.
Решить уравнение — это значит найти все его корни или доказать, что данное уравнение корней не имеет.
Так, уравнение 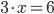 имеет корень
имеет корень 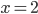 , поскольку
, поскольку 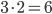 — верное равенство. При этом других корней нет.
— верное равенство. При этом других корней нет.
Основные правила, с помощью которых можно решить уравнение:
• к обеим частям уравнения можно прибавлять одно и то же число или выражение;
• из обеих частей уравнения можно вычитать одно и то же число или выражение;
• можно переносить слагаемое из одной части уравнения в другую, при этом данное слагаемое меняет свой знак на противоположный;
• обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Пример 1. Решите уравнение 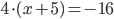 .
.
Решение.
Разделим обе части уравнения на 4.
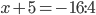 ,
,
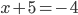 ,
,
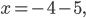
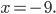
Ответ: —9.
Пример 2. Решите уравнение 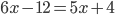 .
.
Решение.
Перенесём 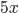 из правой части в левую, изменив знак на противоположный:
из правой части в левую, изменив знак на противоположный:
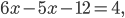
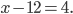
Перенесём (—12) из левой части уравнения в правую, изменив знак на противоположный:
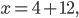
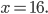
Ответ: 16.
Пример 3. Решите уравнение 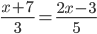 .
.
Решение.
В верной пропорции произведение крайних членов равно произведению средних, поэтому
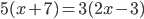 ,
,
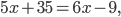
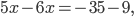
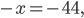
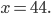
Ответ: 44.
Равенство произведения нулю.
Произведение равно нулю, если
• хотя бы один из сомножителей равен нулю;
• все другие множители при этом имеют смысл.
Например, произведение 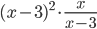 равно нулю только при
равно нулю только при 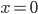 , т. к. при
, т. к. при 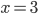 множитель
множитель 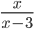 не имеет смысла.
не имеет смысла.
Пример 4. Найдите корни уравнения 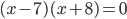 .
.
Решение.
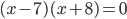 ,
,
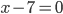 или
или 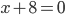 ,
,
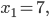
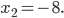
Ответ: -8; 7.
Пример 5. Найдите корни уравнения 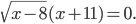
Решение.
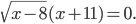
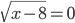 или
или 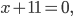
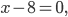
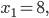
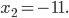
При 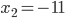 множитель
множитель 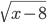 не имеет смысла, так как подкоренное выражение —11 — 8 = —19 < 0. Поэтому заданное уравнение имеет один корень
не имеет смысла, так как подкоренное выражение —11 — 8 = —19 < 0. Поэтому заданное уравнение имеет один корень 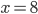 . Ответ: 8.
. Ответ: 8.
Уравнения. Готовимся к ОГЭ по математике. Модуль 1. Урок 21







