Метод возведения обеих частей иррационального уравнения в одну и ту же степень

Метод возведения обеих частей данного иррационального уравнения в одну и ту же степень состоит в следующем:
а) возводят обе части исходного уравнения в одну и ту же степень, предварительно уединив один из радикалов;
б) с учетом тождества

(где а ≥ 0, если n — четное; a є R, если n — нечетное) получают уравнение f(x) = φ(x);
в) решают уравнение f(x) = φ(х) и делают проверку, которая в основном осуществляется с помощью подстановки найденных значений переменной в исходное уравнение.
Замечание 1. Если производить только эквивалентные преобразования исходного уравнения, то проверку делать не нужно.
Замечание 2. При натуральном n уравнение

Необходимо учитывать, что нередко записывают:

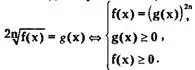
Последняя форма записи решения уравнения

содержащая лишнее неравенство f(x)≥0, как правило, легче усваивается, чем предыдущая, т. к. она более наглядная и включает ОДЗ (f(x)≥0).
Замечание 3.

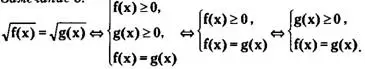
Из приведенных выше трех систем выбирают обычно ту, где проще решить неравенство (f(x)≥0 или g(x)≥0). Если же оба неравенства f(x)≥ 0 и g(x) ≥ 0 решить несложно, то можно выбрать первую систему, которая, хотя и содержит одно лишнее неравенство, является более наглядной, чем вторая или третья системы.
Пример 1. Решить уравнение

Решение. Приведем два варианта решения.
I вариант решения (с проверкой найденных корней).
Возведя в квадрат обе части исходного уравнения, получим Зх - 6 = 9 - 2х <=> 5х = 15 <=> х = 3.
Проверка. При х = 3

Отсюда х = 3 является корнем заданного уравнения.
Ответ: {3}.
II вариант решения (с помощью эквивалентных преобразований).

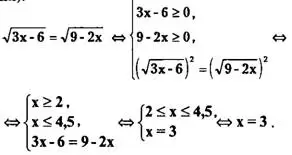
Ответ: {3}.
Пример 2. Решить уравнение

Решение. Приведем два варианта решения.
I вариант решения (с проверкой найденных корней).
Возведя в квадрат обе части исходного уравнения, получим
х3 -2х2 -х + 3 = 4х-3<=>х3-2х2 -5х + 6 = 0. Подбором находим один из корней х=1, а затем, разделив «углом» х3 -2х2 -5х + 6 на (х—1), получим
x³ - 2х² - 5х + 6 = (х -1)(х² - х - 6) = (х -1)(х - 3)(х + 2) = 0 <=> x₁=1; х₂=3; х₃ = -2.
Проверка показывает, что корни x₁ = 1 и х₂ = 3 удовлетворяют исходному уравнению, а корень х₃ = -2 является посторонним.
Ответ: {1;3}.
II вариант решения (с помощью эквивалентных преобразований).

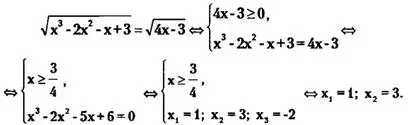
В процессе решения исходного уравнения мы выбрали систему, содержащую более простое неравенство 4х-3≥0, неравенство же х³ - 2х² - х + 3= 0 решать довольно-таки затруднительно, т. к. х³-2х²-х+3=0 не имеет корней среди целых чисел.
Ответ: {1;3}.
Пример 3. Решить уравнение

Решение. Возведя в квадрат обе части исходного уравнения, получим
х⁷-х⁵+1 = х⁷-х⁵+х² <=> 1 = х² <=> х₁ =1; х₂ =-1.
Проверка показывает, что оба корня удовлетворяют исходному уравнению. Заметим, что пример 3 решать с помощью эквивалентных преобразований чрезвычайно трудно, т. к. решение неравенств х⁷-х⁵+1>О и х⁷-х⁵+х²>О может вызвать большие затруднения.
Ответ: {1;-1}.
Пример 4. Решить уравнение

Решение. Решим уравнение двумя способами.
I способ (с проверкой найденных корней).
Возведя обе части исходного уравнения в квадрат, получаем

<=> х + 11 = 1-2х + х² <=> х² -Зх-10 = 0 <=> x₁ = -2, x₂ = 5; x₁,x₂∈D.
Проверка. При x₁=-2

1-x₁ = 1-(-2) = 3, 3 = 3 => x₁ = -2 является корнем исходного уравнения.
При х₂ = 5

1-х₂ = 1-5 = -4;
4≠-4 => х₂ = 5 — лишний корень, хотя x₂∈D.
Ответ: {-2}.
II способ (с помощью эквивалентных преобразований).


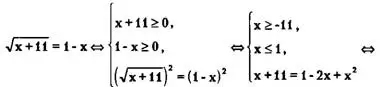
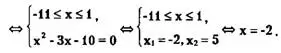
Ответ: {-2}.
Замечание 4. Если быть более точным, то


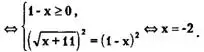
Хотя такая форма записи решения (без х + 11 ≥0)и является более короткой, однако она менее наглядна.
Пример 5. Решить уравнение

Решение. Возведем обе части исходного уравнения в шестую степень, получим:
х - 20 = 2⁶, откуда х = 20 + 2⁶ = 20 + 64 = 84 .
Проверка. Подставив х=84 в исходное уравнение, получаем

т. е. 2 = 2 — верное равенство => х=84 является корнем.
Ответ: {84}.
Пример 6. Решить уравнение

Решение. Уединим один из радикалов, а затем возведем обе части уравнения в квадрат


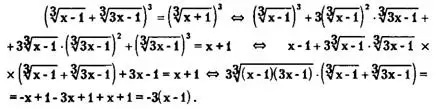
<=> х-3 = 1 <=> х = 4 .
Проверка. При х=4

2 = 2 <=> х = 4 является корнем исходного уравнения.
Ответ: {4}.
Пример 7. Решить уравнение

Решение. ОДЗ исходного уравнения — вся числовая прямая, т.е. х ∈ R. Возведем обе части исходного уравнения в куб

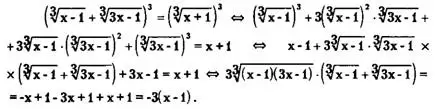
Заменим выражение

являющееся левой частью исходного уравнения правой частью исходного уравнения, т. е. положим

Получим

Разделим обе части последнего уравнения на 3 и возведем Обе части в куб:
(x-1)(3x-1)(x+1)=-(x-1)³ <=> (x-1)(3x-1)(x+1)+4(х-1)³=0 <=> (x-1)[(Зx-1)(х+1)+(x-1)²]=0 <=>

В полученной совокупности уравнений уравнение (а) имеет Корень х=1, а уравнение (б) эквивалентно следующему:
Зх² +Зх-х-1 + х²-2х + 1 = 0 <=> 4х² = 0 <=> х²=0 <=> х = 0.
Проверка. При х = 1


является корнем исходного уравнения.
При х=0


=> х=0 является посторонним корнем.
Этот посторонний корень (х = 0) появился в результате замены левой части исходного уравнения на не равную ей тождественно правую часть, т. е. использование условия исходного уравнения, вообще говоря, не приводит к уравнению, эквивалентному исходному.
Ответ: {1}.
Приведенные выше примеры показывают, что нахождение ОДЗ уравнения не гарантирует нас от появления посторонних корней, то есть не избавляет от необходимости делать проверку полученных в результате решения уравнения корней. Эта проверка, как уже отмечалось, является излишней только в тех случаях, когда в процессе решения уравнения применяются только эквивалентные преобразования.
Как уже отмечалось, находить ОДЗ иногда бывает полезным и можно привести немало примеров, когда знание ОДЗ существенно упрощает решение.
Пример 8. Решить уравнение

Решение. Найдем множество D — область допусти¬мых значений (ОДЗ) исходного уравнения

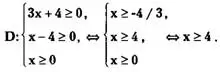
Возведя обе части исходного уравнения в квадрат, получаем

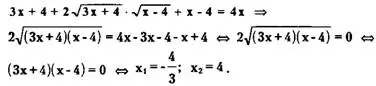
Проверка. Так как x₁=-4/3 ∉ D, то он является посторонним корнем исходного уравнения. Этот посторонний корень не нуждается в проверке.
При x₂ = 4


=> x₂ = 4 является корнем иходного уравнения.
Таким образом, нахождение ОДЗ оказалось полезным, так как позволило не производить проверку постороннего
корня x₁=-4/3, не принадлежащего ОДЗ.
Ответ: {4}.