Решение иррациональных уравнений. Метод введения новых переменных

Пример 1. Решить уравнение

Решение. Сделаем замену переменной, положив



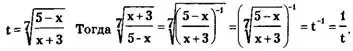
Отсюда получаем
(t² +1)/t = 2 <=> t² - 2t +1 = 0 <=> (t -1)² = 0 <=> t = 1.
Так как производились только эквивалентные преобразования, то исходное уравнение равносильно следующему:
<=>5-х = х + 3<=>5-3= х + х <=> 2 = 2х <=> х = 1.
Проверка. Поскольку уравнение

равносильно исходному уравнению, то найденный корень можно не проверять или проверять подстановкой в уравнение

При х = 1 имеем

является корнем уравнения

а значит и исходного уравнения.
Ответ: {1}.
Пример 2. Решить уравнение

Решение. Преобразуем исходное уравнение к виду

Положив

получаем t² +t -12 = 0 <=> t₁ = 3, t₂ = -4. Взяв t₁ = 3 =>
<=> x²-3x+5 = 9 <=> х²-Зх-4 = 0 <=> x₁ = 4, х₂ = -1. Взяв t₂ = -4, получим

т. к. корень четной степени есть число неотрицательное.
Проверка. Поскольку исходное уравнение эквивалентно уравнению

то корни можно проверять подстановкой в уравнение

Эта подстановка показывает, что x₁ = 4, х₂ = -1 являются корнями этого, а значит и исходного уравнения. Ответ: {4, -1}.
Пример 3. Решить уравнение

Решение. D≥0. Преобразуем выражения, стоящие в левой части исходного уравнения.

Положив
получаем
Отсюда исходное уравнение при t ≥ 0 эквивалентно уравнению
t²-26t = 27 <=> t²-26t-27 = 0 <=> t₁ = 27, t₂=-1.
Так как t ≥ 0, то t₂ = -1 есть посторонний корень. Взяв


Проверка. Поскольку исходное уравнение эквивалентно уравнению то проверку можно производить, подставляя х = 59049 в это уравнение. При

=> х = 59049 является корнем уравнения а значит, и исходного уравнения.
Ответ: {59049}.
Пример 4. Решить уравнение

Решение. ОДЗ исходного уравнения х>0. Заметим, что

Сделав замену
получаем t⁵+2t⁴-t⁶=0 <=>

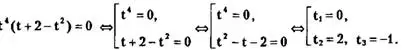
Положив
Положив
Поскольку t > 0 => t₃ = -1 является посторонним корнем.
Проверка. При

является корнем. При


является корнем.
Ответ: {0; 256}
Пример 5. Решить уравнение

Решение.
Положив
получаем

Возведем (U+V) в пятую степень, пользуясь треугольником Паскаля:

Проверка. При

является корнем.
При
является корнем.
Ответ: {-1/2; 1/2}