Непрерывность и точки разрыва функции. Примеры. Практикум по математическому анализу. Урок 22

Пример 1. Показать, что элементарные функции:
1) $\displaystyle y=2x^{2}-1$ ; 2) $\displaystyle v=\textrm{cosec}\: x$ .
непрерывны во всей своей области определения.
Решение. Найдем область определения функции и затем убедимся, исходя из определения непрерывности, что функция будет непрерывна в этой же области.
1) Областью определения функции $y$ является вся числовая ось. Далее, придадим аргументу $x$ произвольное приращение $\displaystyle \Delta x$ и, подставив в данное выражение функции вместо $x$ наращенное значение $\displaystyle x+\Delta x$ , найдем наращенное значение функции:
$\displaystyle y+\Delta y=2(x+\Delta x)^{2}-1$ .
Вычитая из этого наращенного значения функции ее первоначальное значение, найдем приращение функции:
$\displaystyle \Delta y=2(x+\Delta x)^{2}-1-(2x^{2}-1)=4x\Delta x+2\Delta x^{2}.$
Пусть теперь $\displaystyle \Delta x \to 0$ . Тогда при любом значении $x$ , $\displaystyle \underset{\Delta x \to 0}{\textrm{lim}}\Delta y=0$ . Следовательно, согласно определению непрерывности, функция $y$ будет непрерывна при любом значении $x$ , т. е. во всей своей области определения.
2) Тригонометрическая функция $\displaystyle \textrm{cosec}\: x$ определена на всей числовой оси, за исключением точек $\displaystyle x=k\pi ,\; k=0,\pm 1,\pm 2,...$ .
Повторяя указанные выше рассуждения, найдем приращение функции $\displaystyle \Delta v$ и затем его предел при $\displaystyle \Delta x \to 0$ :
$\displaystyle \Delta v=\textrm{cosec}\: (x+\Delta x)-\textrm{cosec}\: x=\frac{1}{\sin (x+\Delta x)}-\frac{1}{\sin x}=\frac{\sin x-\sin (x+\Delta x)}{\sin (x+\Delta x)\sin x}=\frac{2\cos \left ( x+\frac{\Delta x}{2} \right )\sin \left ( -\frac{\Delta x}{2} \right )}{\sin (x+\Delta x)\sin x};$
$\displaystyle \underset{\Delta x \to 0}{\textrm{lim}}\Delta v=\underset{\Delta x \to 0}{\textrm{lim}}\frac{2\cos \left ( x+\frac{\Delta x}{2} \right )}{\sin (x+\Delta x)\sin x}\cdot \underset{\Delta x \to 0}{\textrm{lim}}\sin \left ( -\frac{\Delta x}{2} \right )=\frac{2\cos x}{\sin ^{2}x}\cdot 0=0$ .
при всех значениях $x$ , кроме $\displaystyle x=k\pi ,\; k=0,\pm 1,\pm 2,...$ .
Следовательно, область непрерывности и область определения элементарной функции $\displaystyle \textrm{cosec}\: x$ полностью совпадают.
Пример 1. Дана функция. Найти ее точки разрыва, если они существуют, и скачок функции в каждой точке разрыва:
1) $\displaystyle f_{1}(x)=\frac{1}{x^{2}-4}$ ;
2) $\displaystyle f_{2}(x)=\frac{3x-5}{x^{2}+2x+10}$ ;
3) $\displaystyle f_{3}(x)=\textrm{arcctg}\frac{1}{x}$ ;
4) $\displaystyle f_{4}(x)=\frac{\left | x-3 \right |}{x-3}$ ;
5) $\displaystyle f_{5}(x)=\textrm{lg}(x^{2}+3x)$ .
Решение. 1) Функция $\displaystyle f_{1}(x)$ определена, т. е. может быть вычислена при всех значениях $x$ , кроме $\displaystyle x=\pm 2$ . Эта функция элементарная, поэтому она непрерывна во всей области своего определения: $\displaystyle -\infty <x<-2,\; -2<x<2,\; 2<x<+\infty$ . Она не определена в точках $\displaystyle x_{1}=-2$ и $\displaystyle x_{2}=2$ , но определена вблизи этих точек. Вследствие этого, ввиду несоблюдения 1-го условия непрерывности, данная функция в точках $\displaystyle x_{1}$ и $\displaystyle x_{2}$ имеет разрывы. Для определения скачка функции в найденных ее точках разрыва вычислим односторонние пределы этой функции при стремлении аргумента $x$ к точкам разрыва слева и справа:
а) $\displaystyle \underset{x \to -2-0}{\textrm{lim}}\frac{1}{x^{2}-4}=+\infty ,$
так как при $\displaystyle x \to -2-0$ величина $\displaystyle x^{2}-4$ является положительной бесконечно малой, а обратная ей величина $\displaystyle \frac{1}{x^{2}-4}$ является положительной бесконечно большой;
$\displaystyle \underset{x \to -2+0}{\textrm{lim}}\frac{1}{x^{2}-4}=-\infty$ ,
так как при $\displaystyle x \to -2+0$ величина $\displaystyle x^{2}-4$ является отрицательной бесконечно малой, а обратная ей величина является отрицательной бесконечно большой.
Следовательно, в точке $\displaystyle x=-2$ функция имеет бесконечный разрыв (рис. 1).

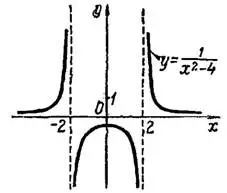
Рис.1

б) $\displaystyle \underset{x \to -2-0}{\textrm{lim}}\frac{1}{x^{2}-4}=-\infty$ ,
так как при $\displaystyle x \to -2-0$ величина $\displaystyle x^{2}-4$ есть отрицательная бесконечно малая, а обратная ей величина есть отрицательная бесконечно большая;
$\displaystyle \underset{x \to -2+0}{\textrm{lim}}\frac{1}{x^{2}-4}=+\infty$ ,
так как при $\displaystyle x \to -2+0$ величина $\displaystyle x^{2}-4$ есть положительная бесконечно малая, а обратная ей величина есть положительная бесконечно большая.
Следовательно, и в точке 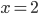$x=2$ разрыв функции бесконечный.
2) Элементарная функция $\displaystyle f_{2}(x)$ определена на всей числовой оси (хотя она дробная, но корни знаменателя комплексные). Поэтому она и непрерывна на всей числовой оси, т. е. не имеет точек разрыва.
3) Элементарная функция $\displaystyle f_{3}(x)$ определена, а следовательно, и непрерывна на всей числовой оси, кроме точки $x=0$ . В точке $x=0$ функция имеет разрыв, поскольку она определена в любой окрестности этой точки, за исключением самой точки.
Найдем односторонние пределы функции в этой точке:
$\displaystyle \underset{x \to -0}{\textrm{lim}}\textrm{arcctg}\frac{1}{x}=\textrm{arcctg}(-\infty )=\pi ;$
$\displaystyle \underset{x \to +0}{\textrm{lim}}\textrm{arcctg}\frac{1}{x}=\textrm{arcctg}(+\infty )=0.$
Следовательно, разрыв функции конечный (рис. 2); при $x=0$ она имеет конечный скачок
$\displaystyle \underset{x \to +0}{\textrm{lim}}f_{3}(x)-\underset{x \to -0}{\textrm{lim}}f_{3}(x)=0-\pi =-\pi.$

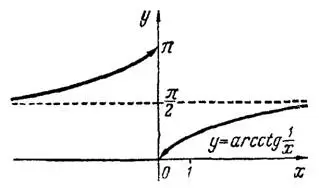
Рис.2

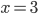4) Функция $\displaystyle f_{4}(x)$ определена и непрерывна на всей числовой оси, кроме точки $x=3$ . Из этого следует, что в точке 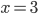$x=3$ функция имеет разрыв.
Исследуем эту точку разрыва:
$\displaystyle \underset{x \to 3-0}{\textrm{lim}}\frac{\left | x-3 \right |}{x-3}=-1,$
так как при всяком значении $x<3$ эта функция равна -1;
$\displaystyle \underset{x \to 3+0}{\textrm{lim}}\frac{\left | x-3 \right |}{x-3}=1,$
так как при всяком значении $x>3$ эта функция равна +1.
Следовательно, в точке 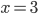$x=3$ функция имеет конечный разрыв (рис. 3); ее скачок в этой точке разрыва конечный:
$\displaystyle \underset{x \to 3+0}{\textrm{lim}}f_{4}(x)-\underset{x \to 3-0}{\textrm{lim}}f_{4}(x)=1-(-1)=2.$

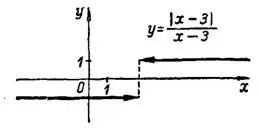
Рис.3

5) Логарифмическая функция $\displaystyle y=\textrm{lg}u$ определена только для положительных значений своего аргумента $u$ . Поэтому элементарная функция $\displaystyle f_{5}(x)=\textrm{lg}(x^{2}+3x)$ будет определена и непрерывна для значений $x$ , удовлетворяющих неравенству $\displaystyle x^{2}+3x>0$ . Решая это неравенство, найдем область определения и область непрерывности функции, — она будет состоять из двух интервалов числовой оси:
$\displaystyle -\infty <x<-3$ и $\displaystyle 0<x<+\infty$ . Во всех точках отрезка $\displaystyle -3\leq x\leq 0$ данная функция не определена, однако точками ее разрыва являются только граничные точки $x=-3$ и $x=0$ . В этих граничных точках функция не определена, но она определена в сколь угодно близких точках слева от точки $x=-3$ и справа от точки $x=0$ . Все остальные внутренние точки отрезка [— 3; 0], в которых функция также не определена, как и в точках $x=-3$ и $x=0$ , не являются точками разрыва потому, что вблизи этих внутренних точек функция не определена.

Точка, в которой функция не определена, будет точкой разрыва функции лишь при условии, если функция определена, хотя бы с одной стороны вблизи этой точки.
Найдя односторонние пределы функции при стремлении $x$ к точкам разрыва изнутри области определения функции
$\displaystyle \underset{x \to -3-0}{\textrm{lim}}(x^{2}+3x)=\textrm{lg}0=-\infty ;\; \underset{x \to +0}{\textrm{lim}}(x^{2}+3x)=\textrm{lg}0=-\infty$ ,
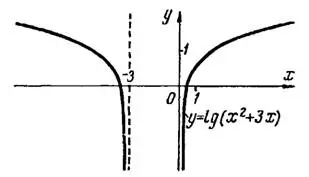
заключаем, что в точках $x=-3$ и $x=0$ функция имеет бесконечные разрывы (рис. 4).