Частные производные функции многих переменных
Функцию  можно дифференцировать по каждому из ее аргументов, считая при этом все остальные аргументы постоянными.
можно дифференцировать по каждому из ее аргументов, считая при этом все остальные аргументы постоянными.
Производная от функции  по
по 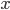 , взятая в предположении, что все остальные аргументы
, взятая в предположении, что все остальные аргументы  являются постоянными, называется частной производной от
являются постоянными, называется частной производной от  по
по 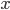
и обозначается  или
или  , т. е.
, т. е.

Аналогично определяются и обозначаются частные производные от функции  по каждому из остальных ее аргументов.
по каждому из остальных ее аргументов.
Частные производные функции многих переменных находятся по известным правилам дифференцирования функции одной независимой переменной.
Пример 1. Найти частные производные от функций:
1)  ;
;
2)  ;
;
3) ![\displaystyle v=\sqrt[x]{e^{y}}](https://math-helper.ru/wp-content/plugins/latex/cache/tex_92f788522511f1bfce8b5ce1001ea8a9.gif) .
.
Решение.
1) Считая  функцией только одного аргумента
функцией только одного аргумента 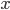 , находим
, находим  .
.
Аналогично, считая  функцией только
функцией только 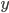 , получим
, получим  .
.
2) Считая  функцией только
функцией только 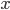 , затем только
, затем только 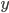 и только
и только  , получим:
, получим:

3) Заменяя корень степенью с дробным показателем и затем дифференцируя по каждой из двух переменных, получим:

Пример 2. Вычислить значения частных производных данных функций при указанных значениях аргументов:
1) 
2) 
Решение.
1) По формулам дифференцирования находим частные производные:

Полагая  , получим
, получим 
2) Находим производные, затем вычисляем их частные значения в указанной точке:

Пример 3. Проверить, что функция  удовлетворяет уравнению
удовлетворяет уравнению  .
.
Решение. Тождественно преобразуем данную функцию и находим ее частные производные по 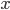 и по
и по 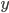 :
:

Подставляя  и
и  в данное уравнение, получим тождество
в данное уравнение, получим тождество  Это значит, что данная функция удовлетворяет данному уравнению (является его решением).
Это значит, что данная функция удовлетворяет данному уравнению (является его решением).







