Функции многих переменных, их обозначение и область определения (теория). Практикум по математическому анализу. Урок 98

Функции многих переменных, их обозначение и область определения (теория)
Переменная $u$ называется функцией $n$ переменных (аргументов) $x,y,z,...,t$, если каждой системе значений $x,y,z,...,t$ из области их изменения, соответствует определенное значение $u$.
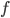Функциональная зависимость $u$ от $x,y,z,...,t$ символически обозначается: $u=f(x,y,z,...,t)$, где после символа функции (которым может быть не только буква $f$, но и другие буквы) в скобках указываются все переменные, от которых зависит данная функция.

Частное значение функции $P(x,y,z,...,t)$ при $x=a,\: y=b,\: z=c,...,t=l$ обозначается $P(a,b,c,...,l)$. Например, если $\displaystyle F(x,y,z)=\frac{3x}{y-\lg z}$, то $\displaystyle F(-2,3,10)=\frac{-6}{3-1}=-3.$

Геометрически, каждая система значений двух переменных $x,y$ изображается точкой на плоскости, а функция двух переменных $z=f(x,y)$ — некоторой поверхностью в пространстве; система значений трех переменных $x,y,z$ изображается точкой в пространстве (Обычно значения переменных рассматриваются как абсцисса, ордината и апликата точки в прямоугольной системе координат.)

Система значений четырех и большего числа переменных не имеет геометрического изображения. Однако, в целях общности, для упрощения записей и рассуждений, систему значений любого числа $n$ переменных $x,y,z,...,t$ называют точкой $n$-мерного пространства $M(x,y,z,...,t)$, а функцию $u$, зависящую от $n$ переменных, называют функцией точки $n$-мерного пространства $u=f(x,y,z,...,t)=f(M)$.

Областью определения (существования) функции называется совокупность всех точек, в которых она имеет определенные действительные значения.

Для функции двух переменных $z=f(x,y)$ область определения представляет некоторую совокупность точек плоскости, а для функции трех переменных $u=F(x,y,z)$ — некоторую совокупность точек пространства.