Приближенное вычисление определенных интегралов (примеры). Практикум по математическому анализу. Урок 97

Пример 1. Вычислить интеграл $\displaystyle \int_{1}^{9}\sqrt{6x-5}dx$ по формуле Ньютона — Лейбница и по приближенным формулам прямоугольников, трапеций и Симпсона, разбивая интервал интегрирования на 8 равных частей. Затем оценить в процентах погрешность результатов, полученных по приближенным формулам.
Решение. По формуле Ньютона — Лейбница

$$\displaystyle I=\int_{1}^{9}\sqrt{6x-5}dx=\frac{1}{6}\int_{1}^{9}(6x-5)^{\frac{1}{2}}d(6x-5)=\frac{1}{9}(6x-5)^{\frac{3}{2}} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{1}^{9}=38.$$

Далее делим интервал интегрирования [1; 9] на 8 равных частей, находим длину одной части $h=1$, точки деления $x_{i}$ значения $y_{i}$ подынтегральной функции $y=\sqrt{6x-5}$ в этих точках:

$x_{0}=1\; \; \; y_{0}=\sqrt{1}=1,0000$
$x_{1}=2\; \; \; y_{1}=\sqrt{7}=2,6458$
$x_{2}=3\; \; \; y_{2}=\sqrt{13}=3,6056$
$x_{3}=4\; \; \; y_{3}=\sqrt{19}=4,3589$
$x_{4}=5\; \; \; y_{4}=\sqrt{25}=5,0000$
$x_{5}=6\; \; \; y_{5}=\sqrt{31}=5,5678$
$x_{6}=7\; \; \; y_{6}=\sqrt{37}=6,0828$
$x_{7}=8\; \; \; y_{7}=\sqrt{43}=6,5574$
$x_{8}=9\; \; \; y_{8}=\sqrt{49}=7,0000$

и вычисляем интеграл по приближенным формулам.

По формуле прямоугольников

$$\displaystyle \int_{a}^{b}ydx\approx h(y_{0}+y_{1}+y_{2}+...+y_{n-1})=h\sum_{i=0}^{n-1}y_{i}\; \; \; (1)$$

$$\displaystyle I\approx \sum_{i=0}^{7}y_{i}=34,8183.$$

Абсолютная ошибка этого приближенного значения (по недостатку) равна 3,1817, а относительная (процентная) ошибка равна $\displaystyle \frac{3,1817\cdot 100}{38}\approx 8,37 \%.$

По формуле прямоугольников

$$\displaystyle \int_{a}^{b}ydx\approx h(y_{1}+y_{2}+y_{3}+...+y_{n})=h\sum_{i=1}^{n}y_{i}.\; \; \; (1a)$$

$\displaystyle I\approx \sum_{i=1}^{8}y_{i}=40,8183$.

Здесь абсолютная ошибка (по избытку) равна 2,8183, а относительная $\displaystyle \frac{2,8183\cdot 100}{38}\approx 7,42\%$.
По формуле трапеций $\displaystyle I\approx 4+\sum_{i=1}^{7}y_{i}=37,8183.$

Абсолютная ошибка этого результата составляет 0,1817, а относительная $\displaystyle \frac{0,1817\cdot 100}{38}\approx 0,48\%$.

По формуле Симпсона

$$\displaystyle I\approx \frac{1}{3}(8+4\cdot 19,1299+2\cdot 14,6884)\approx 37,9655.$$

Абсолютная ошибка составляет всего 0,0345, а относительная $\displaystyle \frac{0,0345\cdot 100}{38}\approx 0,09\%$.

Пример 2. По формуле Симпсона вычислить приближенное значение интеграла $\displaystyle \int_{0}^{\frac{\pi }{2}}\cos xdx$ с точностью до 0,00001.
Решение. Вначале определим, на какое число $n$ частей следует разделить интервал интегрирования $\left [ 0;\frac{\pi }{2} \right ]$, чтобы получить заданную точность вычисления.
Полагая погрешность $\delta (n)$ формулы Симпсона меньше $10^{-5}$, имеем

$$\displaystyle \frac{(b-a)^{5}}{180n^{4}}y_{max}^{(4)}<10^{-5}.$$

Подставляя $\displaystyle a=0,\, b=\frac{\pi }{2},\: y_{max}^{(4)}=1$ (наибольшее значение $\displaystyle \left | y^{(4)} \right |=\left | \cos x \right |$ в интервале $\left [ 0;\frac{\pi }{2} \right ]$), получим

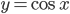Далее, полагая $n=10$ (ближайшее четное число, большее 8,5) определяем точки деления $x_{i}$ и соответствующие им значения $y_{i}$ подынтегральной функции $y=\cos x$ (с одним лишним десятичным знаком, $\pi \approx 3,141592$):

$x_{0}=0,000000\; \; \; y_{0}=1,000000$
$x_{1}=0,157080\; \; \; y_{1}=0,987688$
$x_{2}=0,314159\; \; \; y_{2}=0,951057$
$x_{3}=0,471239\; \; \; y_{3}=0,891007$
$x_{4}=0,628318\; \; \; y_{4}=0,809017$
$x_{5}=0,785398\; \; \; y_{5}=0,707107$
$x_{6}=0,942478\; \; \; y_{6}=0,587785$
$x_{7}=1,099557\; \; \; y_{7}=0,453991$
$x_{8}=1,256637\; \; \; y_{8}=0,309017$
$x_{9}=1,413716\; \; \; y_{9}=1=0,156435$
$x_{10}=1,570796\; \; \; y_{10}=0,000000$

Подставляя в формулу Симпсона, получим искомое значение интеграла с точностью до $10^{-5}$:

$$\displaystyle \int_{0}^{\frac{\pi }{2}}\cos xdx\approx 0,0523599(1+4\cdot 3,196228+2\cdot 2,656876)\approx 1,00000.$$

В решении этой задачи показано, что для вычисления интеграла с заданной точностью, когда известно аналитическое выражение интегрируемой функции, можно, исходя из указанных неравенств для оценки погрешности приближенных формул, заранее определить необходимое число делений интервала интегрирования, которое бы обеспечило заданную точность.

Однако во многих случаях аналитическое выражение интегрируемой функции таково, что трудно найти наибольшее значение во всем интервале интегрирования для производных первого, второго или четвертого порядков, которые содержатся в неравенствах, определяющих погрешности формул прямоугольников, трапеций или Симпсона. Поэтому в вычислительной практике вместо указанных неравенств для оценки погрешности приближенного вычисления интегралов часто применяют другие критерии, с которыми можно ознакомиться в специальных пособиях по приближенным вычислениям.