Приближенное вычисление определенных интегралов. Практикум по математическому анализу. Урок 96
Для приближенного вычисления определенных интегралов имеется несколько способов. Если функция  задана формулой или таблицей, то приближенное значение определенного интеграла
задана формулой или таблицей, то приближенное значение определенного интеграла  можно найти следующим путем:
можно найти следующим путем:
1) разделить интервал интегрирования [a;b] точками  на
на  равных частей
равных частей  ;
;
2) вычислить значения подынтегральной функции  в точках деления
в точках деления  ;
;
3) воспользоваться одной из приближенных формул. Наиболее употребительны следующие приближенные формулы, основанные на геометрическом представлении определенного интеграла в виде площади криволинейной трапеции.
I. Формула прямоугольников

или

Геометрически (рис. 1) по этой формуле площадь криволинейной трапеции  , которая соответствует интегралу
, которая соответствует интегралу  , заменяется суммой площадей заштрихованных прямоугольников.
, заменяется суммой площадей заштрихованных прямоугольников.
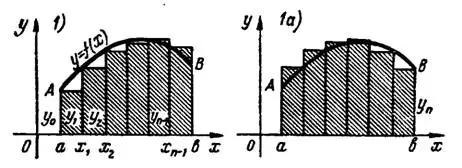
Погрешность формулы прямоугольников

где  — наибольшее значение
— наибольшее значение  в интервале [a,b].
в интервале [a,b].
II. Формула трапеций

Геометрически (рис. 2) по этой формуле площадь криволинейной трапеции заменяется суммой площадей заштрихованных трапеций.
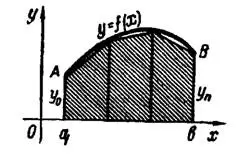
Погрешность формулы трапеций

где  — наибольшее значение
— наибольшее значение  в интервале [a,b].
в интервале [a,b].
III. Формула параболических трапеций (Симпсона);  — число четное.
— число четное.
![\displaystyle \int_{a}^{b}ydx\approx\frac{h}{3}\left [ y_{0}+y_{n}+4(y_{1}+y_{3}+...+y_{n-1})+2(y_{2}+y_{4}+...+y_{n-2}) \right ].\; \; \; (3)](https://math-helper.ru/wp-content/plugins/latex/cache/tex_02e3813a78d86a966275b86c77693e90.gif)
Геометрически (рис. 3) по этой формуле площадь каждой пары вертикальных полосок  заменяется площадью одноименной параболической трапеции, получаемой при замене соответствующего участка кривой
заменяется площадью одноименной параболической трапеции, получаемой при замене соответствующего участка кривой  дугой параболы
дугой параболы  (с вертикальной осью), проходящей через три точки кривой с абсциссами
(с вертикальной осью), проходящей через три точки кривой с абсциссами  и
и  .
.
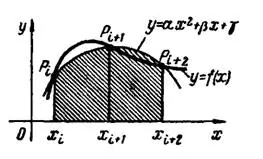
Погрешность формулы Симпсона

где  — наибольшее значение
— наибольшее значение  в интервале [a;b].
в интервале [a;b].
Очевидно, все указанные приближенные формулы будут тем точнее, чем больше взято  , т. е. при достаточно большом значении
, т. е. при достаточно большом значении  посредством каждой из этих формул можно вычислить приближенное значение определенного интеграла с любой желаемой точностью.
посредством каждой из этих формул можно вычислить приближенное значение определенного интеграла с любой желаемой точностью.
При одном и том же значении  обычно вторая формула точнее первой, а третья точнее второй.
обычно вторая формула точнее первой, а третья точнее второй.







