Несобственные интегралы. Урок 95
Интегралы с бесконечными пределами или от разрывных функций называются несобственными.
I. Несобственные интегралы с бесконечными пределами интегрирования определяются посредством предельного перехода:



где
 — произвольное вещественное число.
— произвольное вещественное число.II. Несобственные интегралы от функций с бесконечными разрывами также определяются посредством предельного перехода:
если функция
 имеет бесконечный разрыв в точке
имеет бесконечный разрыв в точке  , принадлежащий отрезку [a;b], и непрерывна во всех других точках этого отрезка, то
, принадлежащий отрезку [a;b], и непрерывна во всех других точках этого отрезка, то
где  и
и  изменяются независимо друг от друга.
изменяются независимо друг от друга.
Несобственные интегралы называются сходящимися или расходящимися, смотря по тому, существуют или нет определяющие их пределы соответствующих определенных (собственных) интегралов.
Пример 1. Найти следующие несобственные интегралы:
1) 
2) 
3) 
4) ![$\displaystyle \int_{-1}^{2}\frac{dx}{\sqrt[3]{(x-1)^{2}}}.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_77e5bcae872181d0df32b8a398f3cd53.gif)
Пояснить решение геометрически.
Решение. 1) Пользуясь равенством (1), имеем

Следовательно, данный несобственный интеграл сходится.
Геометрически, в прямоугольной системе координат, всякий определенный интеграл  дает алгебраическую сумму площадей, ограниченных кривой
дает алгебраическую сумму площадей, ограниченных кривой  , двумя вертикальными прямыми
, двумя вертикальными прямыми  ,
,  и осью
и осью  .
. 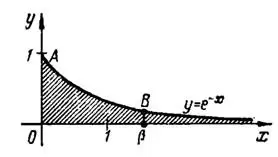
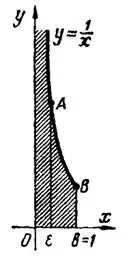
Поэтому, построив кривую  и ее ординаты в точках
и ее ординаты в точках  и
и  (рис.1), получим криволинейную трапецию
(рис.1), получим криволинейную трапецию  , площадь которой
, площадь которой

При  получим трапецию с бесконечным основанием, которая имеет конечную площадь
получим трапецию с бесконечным основанием, которая имеет конечную площадь  .
.
2) Пользуясь определением (3), получим

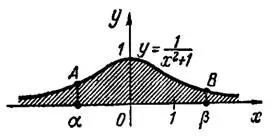
Геометрически (рис.2) интеграл от функции  в пределах от
в пределах от  до
до 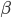 выражает площадь криволинейной трапеции
выражает площадь криволинейной трапеции  , а данный несобственный сходящийся интеграл выражает площадь бесконечной криволинейной трапеции, которая неограниченно простирается влево и вправо и вместе с тем имеет конечную величину
, а данный несобственный сходящийся интеграл выражает площадь бесконечной криволинейной трапеции, которая неограниченно простирается влево и вправо и вместе с тем имеет конечную величину  .
.
3) Здесь при  подынтегральная функция
подынтегральная функция 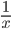 имеет бесконечный разрыв. Согласно определению (4)
имеет бесконечный разрыв. Согласно определению (4)

т. е. этот несобственный интеграл расходится.
Геометрически (рис.3) полученный результат указывает, что площадь криволинейной трапеции 

при  неограниченно возрастает.
неограниченно возрастает.
4) Здесь подынтегральная функция имеет бесконечный разрыв в точке 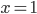 , лежащей внутри отрезка интегрирования [-1;2]. Поэтому, согласно определению (4),
, лежащей внутри отрезка интегрирования [-1;2]. Поэтому, согласно определению (4),
![\displaystyle \int_{-1}^{2}\frac{dx}{\sqrt[3]{(x-1)^{2}}}=\underset{\varepsilon_{1} \to +0}{\lim }\int_{-1}^{1-\varepsilon _{1}}\frac{dx}{\sqrt[3]{(x-1)^{2}}}+\underset{\varepsilon_{2} \to +0}{\lim }\int_{1+\varepsilon _{2}}^{2}\frac{dx}{\sqrt[3]{(x-1)^{2}}}=\lim 3\sqrt[3]{x-1}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{-1}^{1-\varepsilon _{1}}+\lim 3\sqrt[3]{x-1}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{1+\varepsilon_{2}}^{2}=3\lim (\sqrt[3]{-\varepsilon_{1}}-\sqrt[3]{-2})+3\lim (\sqrt[3]{1}-\sqrt[3]{\varepsilon_{2}})=3(\sqrt[3]{2}+1).](https://math-helper.ru/wp-content/plugins/latex/cache/tex_64c863e863f6d21f3be8f3631a69aff3.gif)
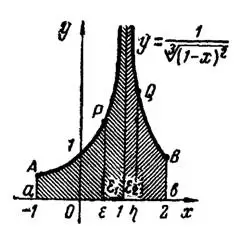
Для графика подынтегральной функции ![\displaystyle y=\frac{1}{\sqrt[3]{(x-1)^{2}}}](https://math-helper.ru/wp-content/plugins/latex/cache/tex_5cc8deaa66201b5a87b3215604213f3a.gif) (рис.4) прямая
(рис.4) прямая 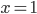 является вертикальной асимптотой. Интегралы от этой функции в пределах от — 1 до
является вертикальной асимптотой. Интегралы от этой функции в пределах от — 1 до  и от
и от  до 2 выражают площади криволинейных трапеций
до 2 выражают площади криволинейных трапеций  и
и  . При
. При  и
и  эти трапеции неограниченно простираются вверх и вместе с тем имеют конечные площади, сумма которых равна найденному значению данного несобственного сходящегося интеграла.
эти трапеции неограниченно простираются вверх и вместе с тем имеют конечные площади, сумма которых равна найденному значению данного несобственного сходящегося интеграла.
Пример 2. Найти несобственные интегралы:
1) 
2) 
Решение.
1) Преобразуем интеграл к новой переменной. Полагая  , получим;
, получим;  при
при  ;
;  при
при 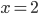 ;
;

Здесь в результате замены переменной данный несобственный интеграл (от функции, имеющей бесконечный разрыв в правом конце интервала интегрирования) преобразовался в собственный интеграл от непрерывной функции и с конечным интервалом интегрирования, который вычислен обычным путем без применения предельного перехода.
Возможно и обратное. При замене переменной собственный интеграл может перейти в несобственный.
2) Согласно определению (1)

К последнему интегралу применяем формулу интегрирования по частям  . Полагая
. Полагая  , получим
, получим  и
и

Подставляя в предыдущее равенство, имеем:

Здесь для нахождения предела последнего слагаемого применено правило Лопиталя.







