Координаты центра тяжести
Центром тяжести совокупности материальных точек называется центр параллельных сил тяжести, приложенных в этих точках.
Для материальной дуги  плоской кривой прямоугольные координаты центра тяжести С определяются формулами
плоской кривой прямоугольные координаты центра тяжести С определяются формулами

где 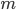 — масса дуги
— масса дуги  ;
;  и
и  — статические моменты этой дуги относительно осей
— статические моменты этой дуги относительно осей  и
и  ;
;  — линейная плотность распределения массы в точке
— линейная плотность распределения массы в точке 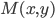 дуги;
дуги;  — дифференциал дуги;
— дифференциал дуги;  и
и  обозначают значения выбранной переменной интегрирования в точках
обозначают значения выбранной переменной интегрирования в точках  и
и  .
.
Если материальная дуга является однородной, то формулы (1) упрощаются: постоянная  выносится за знаки интегралов и сокращается.
выносится за знаки интегралов и сокращается.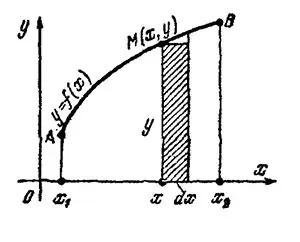
Для материальной однородной криволинейной трапеции, прилежащей к оси  (см. рис. 1),
(см. рис. 1),

Центр тяжести однородной материальной линии или фигуры, имеющей ось симметрии, лежит на этой оси.
Пример 1. Найти центр тяжести четверти окружности  , расположенной в первом квадранте, если в каждой ее точке линейная плотность пропорциональна произведению координат точки.
, расположенной в первом квадранте, если в каждой ее точке линейная плотность пропорциональна произведению координат точки.
Решение. Из уравнения окружности найдем  затем
затем  :
:


Далее вычислим интегралы, содержащиеся в формулах (1), полагая, согласно условию,  :
:



Подставляя значения интегралов в формулы (1), получим

Очевидно, найденная точка не лежит на данной дуге, а расположена ниже ее.
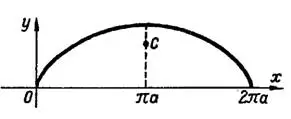
Пример 2. Найти центр тяжести однородной арки циклоиды (рис.2)

Решение. Данная однородная дуга симметрична относительно прямой  . Поэтому центр тяжести дуги лежит на этой прямой, т. е.
. Поэтому центр тяжести дуги лежит на этой прямой, т. е.  . Для определения
. Для определения  найдем дифференциал дуги циклоиды
найдем дифференциал дуги циклоиды

и вычислим интегралы, содержащиеся во второй из формул (1):

![=2\delta a^{2}\left ( \int \sin \frac{t}{2}dt-\int \cos t\sin \frac{t}{2}dt \right ) \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{2\pi }=2\delta a^{2}\left \{ 2\int \sin \frac{t}{2}d\frac{t}{2}-\frac{1}{2}\int \left [ \sin \frac{3}{2}t+\sin \left ( -\frac{t}{2} \right ) \right ]dt \right \} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{2\pi }=](https://math-helper.ru/wp-content/plugins/latex/cache/tex_c784fb7e6705d7fa4c4ac8f5f32f7b88.gif)


По формуле (1), 
Пример 3. Найти центр тяжести однородной фигуры (пластинки), ограниченной параболой  и осями координат.
и осями координат.
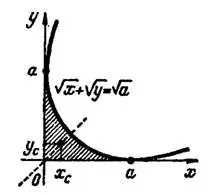
Решение. Данная однородная фигура симметрична относительно биссектрисы первого координатного угла (рис. 3), поэтому  .
.
Вычислим интегралы, содержащиеся в первой из формул (2):


Следовательно, 







