Функции многих переменных, их обозначение и область определения (задачи). Практикум по математическому анализу. Урок 99
Пример 1. Вычислить частное значение функции:
1)  при
при  ;
;
2)  в точке
в точке  .
.
Решение.
1) 
2)  .
.
Пример 2. Построить область 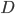 изменения переменных
изменения переменных  и
и  , заданную следующими неравенствами:
, заданную следующими неравенствами:
1) 
2) 
3) 
4) 
Решение. 1) Данным неравенствам удовлетворяют координаты любой точки, находящейся внутри и на границе прямоугольника, стороны которого лежат на прямых  и
и  . Этот прямоугольник и есть область
. Этот прямоугольник и есть область  изменения переменных
изменения переменных  и
и  (рис. 1). Такая область, в которую входит и ее граница, называется замкнутой.
(рис. 1). Такая область, в которую входит и ее граница, называется замкнутой.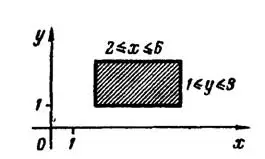
2) Здесь область  есть совокупность всех точек, лежащих внутри эллипса
есть совокупность всех точек, лежащих внутри эллипса  , так как все эти точки, и только они, удовлетворяют данному неравенству (рис. 2). Такая область, в которую не входит ее граница, называется открытой.
, так как все эти точки, и только они, удовлетворяют данному неравенству (рис. 2). Такая область, в которую не входит ее граница, называется открытой.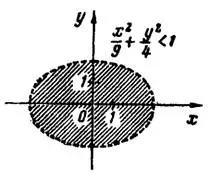
3) Здесь область  есть круговое кольцо, ограниченное окружностями
есть круговое кольцо, ограниченное окружностями  и
и  с общим центром в начале координат и радиусами
с общим центром в начале координат и радиусами  и
и  , рис.3 (замкнутая область).
, рис.3 (замкнутая область).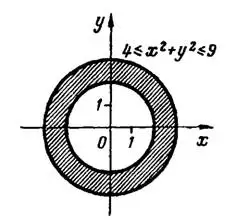
4) Здесь область 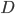 (открытая) ограничена биссектрисой первого координатного угла и осью абсцисс (рис.4).
(открытая) ограничена биссектрисой первого координатного угла и осью абсцисс (рис.4).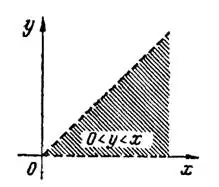
Пример 3. Найти области определения следующих функций:
1) 
2) 
3) 
4) 
5) 
6) 
Решение.
1) Функция  , как и всякая целая рациональная функция, определена (может быть вычислена) при любых значениях
, как и всякая целая рациональная функция, определена (может быть вычислена) при любых значениях  и
и  , т. е. область определения функции
, т. е. область определения функции  есть вся числовая плоскость
есть вся числовая плоскость  ,
,  Геометрическое изображение (график) этой функции есть плоскость, пересекающая координатные оси в точках
Геометрическое изображение (график) этой функции есть плоскость, пересекающая координатные оси в точках  .
.
2) Функция  определена при любой системе значений
определена при любой системе значений  , кроме системы
, кроме системы  , при которой ее знаменатель обращается в нуль. Поэтому областью определения функции
, при которой ее знаменатель обращается в нуль. Поэтому областью определения функции  является вся числовая плоскость, кроме точки
является вся числовая плоскость, кроме точки 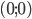 .
.
3) Область определения функции  есть круг с центром в начале координат и радиусом
есть круг с центром в начале координат и радиусом  , включая и его границу — окружность
, включая и его границу — окружность 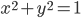 (замкнутая область). Внутри круга подкоренное выражение положительно, на его границе —равно нулю, а вне круга — отрицательно. Графическим изображением функции является полусфера, расположенная над плоскостью
(замкнутая область). Внутри круга подкоренное выражение положительно, на его границе —равно нулю, а вне круга — отрицательно. Графическим изображением функции является полусфера, расположенная над плоскостью  (рис.5).
(рис.5).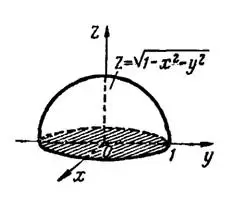
4) Функция 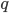 определена в тех и только в тех точках плоскости
определена в тех и только в тех точках плоскости  , координаты которых удовлетворяют неравенству . Все эти точки лежат внутри первого и третьего квадрантов (открытая область).
, координаты которых удовлетворяют неравенству . Все эти точки лежат внутри первого и третьего квадрантов (открытая область).
5) Областью определения функции и является вся плоскость  , за исключением прямой
, за исключением прямой  , в точках которой знаменатель функции и обращается в нуль.
, в точках которой знаменатель функции и обращается в нуль.
6) Область определения функции  есть совокупность систем значений
есть совокупность систем значений  и
и  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  . На плоскости
. На плоскости  эта область представляет полосу, ограниченную параллельными прямыми
эта область представляет полосу, ограниченную параллельными прямыми  и
и  (рис. 6).
(рис. 6).