Применение определенного интеграла в физике. Практикум по математическому анализу. Урок 93

Пример 13. Два одинаковых сосуда имеют форму прямого круглого конуса с вертикальной осью; их расположение и размеры показаны на рис. 1. Оба сосуда наполнены водой и затем опорожняются через небольшие одинаковые круглые отверстия внизу.
Определить время опорожнения каждого сосуда и в какой момент времени вода в обоих сосудах будет на одном уровне, если их опорожнение началось одновременно.
Решение. Полагаем, что время $t$, за которое уровень воды в первом или во втором сосуде понизится на величину $x$, есть некоторая функция $t(x)$ и найдем ее дифференциал $dt$ при изменении $x$ на величину $dx$.

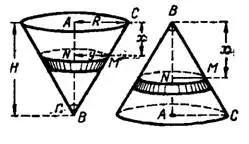
Рис. 1

Пусть понижению уровня воды в сосуде на малую величину $dx$ соответствует малое приращение времени $\Delta t$. Тогда, допуская, что в течение этого малого промежутка времени вода вытекает из сосуда с постоянной скоростью, равной $0,6\sqrt{2g(H-x)}$, найдем, что объем воды, вытекшей за время $\Delta t$ через отверстие в дне площадью $\pi r^{2}$, будет $\displaystyle \Delta v\approx 0,6\pi r^{2}\sqrt{2g(H-x)}\Delta t$.

За это же время $\Delta t$ объем воды в сосуде уменьшится на величину $\displaystyle \Delta v_{1}\approx \pi y^{2}dx$, которая должна быть равна объему вытекшей воды $\Delta v$. Отсюда, из равенства $\Delta v=\Delta v_{1}$, получим

$$\displaystyle \Delta t\approx \frac{y^{2}dx}{0,6r^{2}\sqrt{2g(H-x)}}=dt.$$

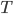Время $T$ полного опорожнения первого или второго сосуда получим, интегрируя $dt$ в пределах от $x=0$ до $x=H$:

$$\displaystyle T=\frac{1}{0,6r^{2}\sqrt{2g}}\int_{0}^{H}\frac{y^{2}dx}{\sqrt{H-x}}.$$

Для вычисления этого интеграла выразим переменную $y$ через переменную $x$.

Из подобия треугольников $ABC$ и $NBM$ имеем:

а) для первого сосуда $\displaystyle \frac{H}{R}=\frac{H-x}{y},\: y=\frac{R}{H}(H-x);$

б) для второго сосуда $\displaystyle \frac{H}{R}=\frac{x}{y},\: y=\frac{R}{H}x.$

Поэтому время $\displaystyle T_{1}$ полного опорожнения первого сосуда будет

$$\displaystyle T_{1}=\frac{R^{2}}{0,6r^{2}H^{2}\sqrt{2g}}\int_{0}^{H}\frac{(H-x)^{2}}{\sqrt{H-x}}dx=\frac{R^{2}}{0,6r^{2}H^{2}\sqrt{2g}}\cdot \frac{2(H-x)^{\frac{5}{2}}}{5} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{H}^{0}=\frac{2R^{2}}{3r^{2}}\sqrt{\frac{H}{2g}}.$$

Время $T_{2}$ полного опорожнения второго сосуда выражается интегралом

$$\displaystyle T_{2}=\frac{R^{2}}{0,6r^{2}H^{2}\sqrt{2g}}\int_{0}^{H}\frac{x^{2}}{\sqrt{H-x}}dx.$$

Вводя новую переменную $z=H-x$, имеем: $dx=-dz;\: z_{1}=H$ при $x=0;\: z_{2}=0$ при $x=H$;

$$\displaystyle \int_{0}^{H}\frac{x^{2}dx}{\sqrt{H-x}}=-\int_{H}^{0}\frac{(H-z)^{2}}{\sqrt{z}}dz=\int_{0}^{H}(H^{2}z^{-\frac{1}{2}}-2Hz^{\frac{1}{2}}+z^{\frac{3}{2}})dz=\frac{16}{15}H^{\frac{5}{2}}.$$

Подставляя найденное значение интеграла, получим $\displaystyle T_{2}=\frac{16R^{2}}{9r^{2}}\sqrt{\frac{H}{2g}}.$

Сопоставив $T_{2}$ и $T_{1}$, взяв их отношение $\displaystyle \frac{T_{2}}{T_{1}}=\frac{8}{3}$, заключаем, что первый сосуд опорожняется значительно (почти в три раза) быстрее второго. При этом, если опорожнение сосудов начинается одновременно, то в начале процесса уровень воды в первом сосуде будет выше, чем во втором, затем наступит момент, когда уровни воды в обоих сосудах сравняются, после чего уровень воды в первом сосуде будет неизменно и все более ниже, чем во втором.

Для определения времени, спустя которое после начала одновременного опорожнения сосудов вода в них будет на одном уровне, найдем зависимость времени $t$ истечения воды от величины $x$ понижения ее уровня для каждого сосуда.

Интегрируя $dt$ в пределах от $x=0$ до $x=x$, получим:
а) для первого сосуда

$$\displaystyle t=b\int_{0}^{x}(H-x)^{\frac{3}{2}}dx=\frac{2}{5}b(H-x)^{\frac{5}{2}} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{x}^{0}=\frac{2}{5}b\left [ H^{\frac{5}{2}}-(H-x)^{\frac{5}{2}} \right ],$$

где $\displaystyle b=\frac{R^{2}}{0,6r^{2}H^{2}\sqrt{2g}};$
б) для второго сосуда

$$\displaystyle t=b\int_{0}^{H}\frac{x^{2}dx}{\sqrt{H-x}}=b\int_{H-x}^{H}(H^{2}z^{-\frac{1}{2}}-2Hz^{\frac{1}{2}}+z^{\frac{3}{2}})dz=b\left ( 2H^{2}z^{\frac{1}{2}}-\frac{4}{3}Hz^{\frac{3}{2}}+\frac{2}{5}z^{\frac{5}{2}} \right ) \left.\begin{matrix} \\ \\ \end{matrix}\right| _{H-x}^{H}=b\left \{ 2H^{2}\left [ H^{\frac{1}{2}}-(H-x)^{\frac{1}{2}} \right ]-\frac{4}{3}H\left [ H^{\frac{3}{2}}-(H-x)^{\frac{3}{2}} \right ]+\frac{2}{5}\left [ H^{\frac{5}{2}}-(H-x)^{\frac{5}{2}} \right ] \right \}.$$

Рассматривая полученные зависимости $t$ от $x$ для первого и второго сосудов как уравнения с искомыми неизвестными $t$ и $x$ и решая их как систему (исключая $t$), найдем:

$$\displaystyle \frac{2}{5}\left [ H^{\frac{5}{2}}-(H-x)^{\frac{5}{2}} \right ]=2H^{2}\left [ H^{\frac{1}{2}}-(H-x)^{\frac{1}{2}} \right ]-\frac{4}{3}H\left [ H^{\frac{3}{2}}-(H-x)^{\frac{3}{2}} \right ]+\frac{2}{5}\left [ H^{\frac{5}{2}}-(H-x)^{\frac{5}{2}} \right ];$$

$$\displaystyle H\left [ H^{\frac{1}{2}}-(H-x)^{\frac{1}{2}} \right ]-\frac{2}{3}\left [ H^{\frac{3}{2}}-(H-x)^{\frac{3}{2}} \right ]=0;$$

По найденному значению $x$ из первого (или второго) уравнения определяем $t$:

$$\displaystyle t=\frac{2}{5}bH^{\frac{5}{2}}\left [ 1-\left ( 1-\frac{\sqrt{3}}{2} \right )^{\frac{5}{2}} \right ].$$

По истечении этого промежутка времени $t$ после начала одновременного опорожнения обоих сосудов вода в них будет на одном уровне

$$\displaystyle h=H-x=H\left ( 1-\frac{\sqrt{3}}{2} \right )\approx 0,15H.$$

Пример 14. Определить массу шара радиуса 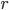$r$, если плотность в каждой его точке пропорциональна расстоянию ее от центра шара.

Решение. Пусть масса шара произвольного радиуса $x$ есть некоторая функция $m(x)$.

При увеличении $x$ на малую величину $dx$ объем $v$ этого шара увеличится на величину $\Delta v$, равную разности объемов шаров с радиусами $x$ и $x+dx$:

$$\displaystyle \Delta v=\frac{4}{3}\pi\left [ (x+dx)^{3}-x^{3} \right ] =\frac{4}{3}\pi (3x^{2}dx+3xdx^{2}+dx^{3})\approx 4\pi x^{2}dx=dv.$$

Допуская, что во всех точках малого объема $dv$ плотность остается неизменной и равной $kx$, найдем приближенную величину его массы $$\displaystyle dm=kxdv=4k\pi x^{3}dx$.

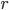Искомую массу $M$ шара радиуса $r$ получим, интегрируя $dm$ в пределах от $x=0$ до $x=r$:

$$\displaystyle M=4k\pi \int_{0}^{r}x^{3}dx=k\pi x^{4} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{r}=k\pi r^{4}.$$