Непрерывность и точки разрыва функции. Практикум по математическому анализу. Урок 21

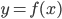Функция $\displaystyle y=f(x)$ называется непрерывной в точке $\displaystyle x_{0}$, если в этой точке бесконечно малому приращению аргумента $\displaystyle x-x_{0}=\Delta x$ соответствует бесконечно малое приращение функции $\displaystyle y-y_{0}=\Delta y$, т. е. если
$\displaystyle \underset{\Delta x \to 0 }{\textrm{lim}}\Delta y=\underset{\Delta x \to 0 }{\textrm{lim}}\left [ f(x_{0}+\Delta x)-f(x_{0}) \right ]=0.$
Этому определению равносильно следующее:
Функция $f(x)$ называется непрерывной в точке $\displaystyle x_{0}$, если при $\displaystyle x \to x_{0}$ предел функции существует и равен ее частному значению в этой точке, т. е. если $\displaystyle \underset{x \to x_{0} }{\textrm{lim}}f(x)=f(x_{0})$.
Для непрерывности функции $f(x)$ в точке $\displaystyle x_{0}$ необходимо и достаточно выполнение следующих условий:
1) функция должна быть определена в некотором интервале, содержащем точку $\displaystyle x_{0}$ (т. е. в самой точке $\displaystyle x_{0}$ и вблизи этой точки);
2) функция должна иметь одинаковые односторонние пределы $\displaystyle \underset{x \to x_{0}-0 }{\textrm{lim}}f(x)=\underset{x \to x_{0}+0 }{\textrm{lim}}f(x);$
3) эти односторонние пределы должны быть равны $\displaystyle f(x_{0})$.

Функция $f(x)$ называется разрывной в точке $\displaystyle x_{0}$, если она определена в сколь угодно близких точках, но в самой точке $\displaystyle x_{0}$ не удовлетворяет хотя бы одному из условий непрерывности.
Разрыв функции $f(x)$ в точке $\displaystyle x_{0}$ называется конечным, или 1-го рода, если существуют конечные односторонние пределы $\displaystyle \underset{x \to x_{0}-0 }{\textrm{lim}}f(x)$ и $\displaystyle \underset{x \to x_{0}+0 }{\textrm{lim}}f(x)$. Все другие случаи разрыва функции называются разрывами 2-го рода; в частности, если хотя бы один из указанных односторонних пределов окажется бесконечным, то и разрыв функции называется бесконечным.
Скачком функции $f(x)$ в точке разрыва $\displaystyle x_{0}$ называется разность ее односторонних пределов $\displaystyle \underset{x \to x_{0}+0 }{\textrm{lim}}f(x)-\underset{x \to x_{0}-0 }{\textrm{lim}}f(x)$, если они различны.
Если точка $\displaystyle x_{0}$ является левой или правой границей области определения функции $f(x)$, то следует рассматривать значения функции соответственно только справа или только слева от этой точки и в самой точке. При этом:
1) если граничная точка $\displaystyle x_{0}$ входит в область определения функции, то она будет точкой непрерывности или точкой разрыва функции, смотря по тому, будет ли предел функции при $\displaystyle x \to x_{0}$ изнутри ее области определения равен или не равен $\displaystyle f(x_{0})$;
2) если граничная точка $\displaystyle x_{0}$ не входит в область определения функции, то она является точкой разрыва функции.
Функция называется непрерывной в некотором интервале, если она непрерывна во всех точках этого интервала.
Все элементарные функции непрерывны в тех интервалах, в которых они определены.

При отыскании точек разрыва функции можно руководствоваться следующими положениями:
1. Элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной во всех точках какого-либо интервала.
2. Элементарная функция может иметь разрыв только в той точке, где она не определена, при условии, если она будет определена хотя бы с одной стороны от этой точки в сколь угодно близких к ней точках.
3. Неэлементарная функция может иметь разрывы как в точках, где она не определена, так и в точках, где она определена; в частности, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов изменения аргумента, то она может иметь разрывы в тех точках, где меняется ее аналитическое выражение (неэлементарные функции могут иметь весьма сложную структуру и могут быть определены и вместе с тем разрывны в каждой точке числовой оси).