Координаты точек. Решение задач. Готовимся к ЕГЭ по математике. Геометрия. Урок 8

Задача 3. Найдите ординату середины отрезка, соединяющего точки 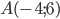$A(-4; 6)$ и $B(2; 4)$ (см. рис. 6).

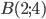Рис.6

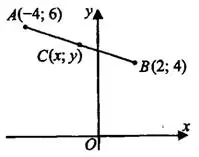
Решение.
Пусть $C(x;y)$ — середина $AB$ . Тогда ордината точки $C$
$\displaystyle y=\frac{y_{A}+y_{B}}{2}=\frac{6+4}{2}=5.$ Ордината равна 5.
Ответ: 5.
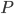Задача 4. Точки $A(-1;-2), B(4;-1), C(6;5)$ и $D$ являются вершинами параллелограмма. Найдите абсциссу точки $P$ пересечения его диагоналей (см. рис. 7).

Рис.7

Решение.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Абсцисса точки $P$ равна
$\displaystyle \frac{x_{A}+x_{C}}{2}=\frac{-1+6}{2}=2,5.$
Ответ: 2,5.
Задача 5. Найдите ординату центра окружности (см. рис. 8), описанной около прямоугольника $ABCD$ , вершины которого имеют координаты соответственно (2;2), (2;—6), (—4;—6), (-4; 2).

Рис.8

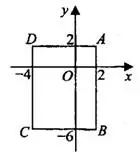
Решение.
Центр описанной окружности прямоугольника лежит на середине диагонали. Найдём ординату середины 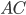$AC$ .
$\displaystyle y=\frac{y_{A}+y_{C}}{2}=\frac{2+(-6)}{2}=-2.$
Ответ: —2.
Задача 6. Точки $O(0; 0), B(8; 2), C(0; 8)$ являются вершинами параллелограмма (см. рис. 9). Найдите ординату точки $M$ .

Рис.9

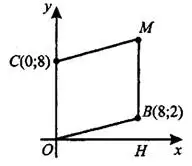
Решение.
Ордината — это координата по оси $Oy$ . Она равна длине отрезка $HM$ (см. рис. 10).

Рис.10

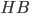$HB$ = 2, так как ордината $B$ равна 2. Поскольку противоположные стороны параллелограмма равны, то $OC = BM = 8$ . Тогда $HM = 2 + 8 = 10$ .
Ответ: 10.
Задача 7. Прямая а проходит через точки с координатами (0;2) и (-4;0). Прямая $b$ проходит через точку с координатами (0;—4) и параллельна прямой $a$ (см. рис. 11). Найдите абсциссу точки пересечения прямой $b$ с осью $Ox$ .

Рис.11

Решение.
1-й способ.
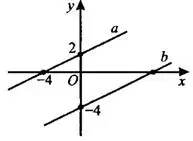
Нарисуем картинку на клетчатой бумаге (см. рис. 12).

Рис.12

Абсцисса точки пересечения прямой $b$ с осью $Ox$ равна длине отрезка $OA$ . Так как прямые параллельны, углы $HCO$ и $ABK$ равны, достроим 2 треугольника $BKT$ и $TMA$ , равных треугольнику $HCO$ .
$OA = BK + TM = 4 + 4 = 8$ .
Ответ: 8.
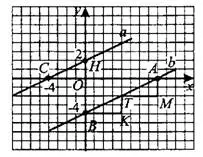
2-й способ.
Треугольники $CHO$ и $BOA$ подобны по трём углам (см. рис. 13), значит, их стороны пропорциональны. $OB : OH = OA : OC$ , тогда $4:2 = OA : 4. OA = 8$ .

Рис.13

Ответ: 8.

Задача 8. Найдите угловой коэффициент прямой, проходящей через точки с координатами (12; 0) и (0; 12) (см. рис. 14).

Рис.14

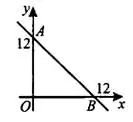
Решение.
Угловой коэффициент прямой равен тангенсу угла, который прямая образует с положительным направлением оси
$Ox$ (там, где на оси стрелочка). В нашей задаче это угол $a$ (см. рис. 15).

Рис.15

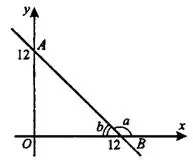
Он тупой, значит, его тангенс отрицательный и по модулю равен тангенсу угла $\displaystyle b=180^{\circ}-a$ . Рассмотрим прямоугольный треугольник $AOB$ с катетами $OA$ = 12 и $OB$ = 12. Тангенс угла $b$ равен $\displaystyle \frac{OA}{OB}=\frac{12}{12}=1$ . Тангенс угла $a$ равен —1. Угловой коэффициент прямой равен —1.
Ответ: —1.