Решение задач на основные геометрические фигуры: точку, прямую, плоскость. Отрезок. Луч. Числовой луч. Шкала. Виды шкал. Урок №11
Если на лист бумаги поставить острие карандаша, получим изображение точки. Точка обозначается заглавной буквой латинского алфавита. Читают: «Точка А», «точка В», «точка С». Точка не имеет ни длины, ни ширины.
Если часть листа бумаги закрасить, тогда чертой, которая отделяет окрашенную часть от неокрашенные, будет линия. Такая линия имеет длину, но не имеет ширины.
Линии бывают кривые, ломаные, прямые.
Для проведения прямых линий используют линейку. Прямая линия не имеет ни начала, ни конца, поэтому на чертеже можно изобразить лишь часть прямой. Прямую линию обозначают одной малой буквой или двумя большими буквами латинского алфавита.
Читают: «Прямая а», «прямая АВ», «прямая ВА», «прямая СА)"; «Точка К лежит на прямой СE>», «Прямая СE> проходит через точку А», «Точка М не лежит на прямой b», «Через точку О проходят три прямые».
Поверхность стола, классной доски, стены, оконного стекла дают представление о плоскости. Но эти поверхности имеют края, а у плоскости края нет. Она бесконечна во всех направлениях.
Точки, прямые и многие другие геометрические фигуры размещаются на плоскости.
Две прямые могут иметь только одну общую точку. Такие прямые называются пересекающимися прямыми.
Через две любые точки можно провести прямую, и к тому же одну.
Луч. Отрезок
Обозначим на прямой АВ точку О. Эта точка разделит прямую на две части. Каждую из них называют лучом. Точку О называют началом луча.
Конца у луча нет. При обозначении луча на первом месте пишут начало луча. Любая точка на прямой разделяет прямую на два луча. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу. Луч обозначают также одной малой буквой латинского алфавита.
Построение отрезка заданной длины.
Построим отрезок длиной 5 см.
Для этого:
1) отметим в тетради произвольную точку и обозначим её, например, буквой А;
2) приложим линейку так, чтобы ее ноль совпал с точкой А;
3) отметим точку, совпадающую с делением 5 см на линейке; обозначим эту точку, например, буквой В;
4) соединим точки А и В, получим отрезок АВ, он и будет искомым; длина отрезка АВ равна 5 см.
Запишем: АВ = 5 см.
Числовой луч
Начертим луч Ох и запишем против его начала О число 0. Выберем некоторый отрезок, длину которого выберем за единицу. Такой отрезок называют единичным отрезком. Отложим от начала луча отрезок ОА, равный единичному отрезку. Против точки А запишем число 1. Говорят, что точка А соответствует числу 1 или число 1 изображено точкой А. Для того, чтобы изобразить на лучи число 2, нужно отложить от начала луча один за другим два одиночных отрезка. Отложив от начала луча один за другим три единичных отрезка, получим на луче точку, которая соответствует числу 3 и т.д.
Шкала. Виды шкал и их применение
На линейке, которой мы пользуемся для измерения отрезков, нанесена часть числового луча. Она образует измерительную шкалу. Шкала разделена черточками на равные части, которые называются делениями. Длине каждого деления соответствует определенная единица измерения.
Шкалы могут быть разные по форме, они есть на многих измерительных приборах.
Шкала может быть прямолинейной или криволинейной. Например, шкалы часов, спидометра - криволинейные.
Для того, чтобы прочитать показания шкалы, надо знать цену деления. Чтобы узнать цену деления шкалы, надо от некоторого числа на шкале вычесть число, которое ему предшествует, и разделить полученную разницу на число делений между этими числами.
Полный урок смотрите в следующем видео:
Домашнее задание:
1. Отметь в тетради точку и через нее проведи пять прямых. Отметить их. Можно еще провести прямые, проходящие через эту точку?
2. а) Отметить в тетради точку О. Принимая точку О за начало луча, проведи лучи ОС, ОD, ОP. Можно еще провести лучи с началом в точке О?
б) Отметить точки А и В. Проведи через эти точки прямую. Сколько лучей при этом получилось? Принимая точки А и В за начало луча, обозначь эти лучи.
3. Дан луч ОА: а) проведи луч ОВ так, чтобы он составил прямую с лучом ОА; б) проведи луч OD, который не составляет с лучом OА прямую.
4. На прямой отмечены точки А, В, С. Принимая точки А, В, С за начало луча, запиши все лучи, которые при этом образовались. Запиши отрезки, которые образовались на рисунке.
5. Запиши все отрезки, изображенные на рисунках.
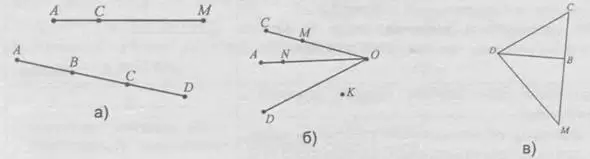
6. AC=58 см, CM=72 см. Вычисли длину отрезка AM.
![]()
7. SN= 6 м, МК = 9 м, NK = 7 м. Вычисли длины отрезков SM, MN, SK.
![]()
8. Земельный участок треугольной формы надо огородить проволочной оградой, которая состоит из двух рядов: верхнего и нижнего. Сколько нужно проволоки, если стороны треугольника 275 м, 494 м, 327 м?
9. Отметить в тетради три точки, не лежащие на одной прямой. Построй все прямые, проходящие через пары этих точек. На сколько частей делят плоскость построенные прямые?
10. Начерти прямую МК, луч NР и отрезки АВ и D так, чтобы прямая МК пересекала отрезки АВ и СD, а отрезок СD лежал на луче NР. Будет ли прямая МК пересекать луч NP?
11. Начерти числовой луч и отметь на нем числа: а) 3, 4, 7 и 9; б) 2, 5, 6, 8 и 12.
12. Запиши координаты точек, отмеченных на числовом луче.
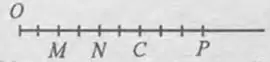
13. Начерти числовой (или координатная) луч и отметь на нем точки A(6), B(5), С(3), D(10) и E(2).
14. Запиши натуральные числа, которые лежат на числовом луче между числами: а) 297 и 305; б) 996 и 1006.
15. На числовом лучи обозначены точки С(14) и D(22). Длина отрезка СD = 4 см. Найди длину единичного отрезка этого луча.
16. Начерти в тетради отрезок длиной 16 см. Над одним концом отрезка напиши 0, а над вторым 16. Раздели отрезок на 4 равные части. Укажи числа, соответствующие каждому штриху, и расположите на полученной шкале числа 2, 5, 6, 9, 12.
17. Найди периметр многоугольника ABDKE, если АВ = 43 см, BD = 42 см, DK = 44 см, KE = 41 см и EA = 40 см.







