Умножение и деление натуральных чисел. Переместительное, сочетательное и распределительное свойства умножения. Урок №7
Умножить число 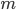 на натуральное число
на натуральное число  означает найти сумму
означает найти сумму  слагаемых, каждое из которых равно
слагаемых, каждое из которых равно 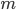 . Выражение
. Выражение  и значение этого выражения называют произведением чисел
и значение этого выражения называют произведением чисел 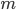 и
и  . Числа
. Числа 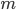 и
и  называют множителями.
называют множителями.
Произведение двух чисел не изменяется при перестановке множителей. Это свойство называется переместительным: от перестановки множителей произведение не меняется.
Сочетательное свойство умножения: чтобы произведение двух чисел умножить на третье число, надо первое число умножить на произведение второго и третьего.
Сумма  множителей, каждый из которых равен 1, равна
множителей, каждый из которых равен 1, равна  .
.
Перед буквенными множителями обычно не пишут знак умножения. Опускают знак умножения и перед скобками. Когда в записи произведении нет скобок, тогда умножения выполняют по порядку слева направо. Произведение читают, называя каждый множитель в родительном падеже.
Действие, с помощью которой по произведению и одному из множителей находят второй множитель, называют делением. Число, которое делят, называют делимым, число, на которое делят, - делителем, результат деления называют частным.
При делении любого числа на 1 получают то же самое число. При делении числа на себя получают единицу.
При делении нуля на число получается ноль.
Полный урок смотрите в следующем видео:
Домашнее задание:
1. Найди значение произведения.
а) 65 •24; б) 243• 14; в) 324•872; г) 305 •406; д) 4606 •709; е) 3127 •35624; ё) 3005 • 6004; ж) 27•100; з) 209 •1000; и) 3400 • 4800.
2. Вычисли: а) 3456:96; 6) 414036:18; в) 6251448:3048.
3. Вычисли:
а) 43475 + 263678 + 98888 • 376; б) (1142600 - 890778): 74 + 309 • 708;
в) (3508 + 492) • 276 -2002 • 307; г) 208896: 68 + (10403 -9896) • 204.
4. Вычисли удобным способом.
а) 43 • 81-23 • 81; 6) 78•24 + 14•24 + 8•24; в) 567:9-477:9;
г) 1134:9-108:9-126:9; д) 4•27•25; е) 13•6•50.
5. Упростите выражение.
а) 230+ 1580 + х; б) 20 -40 -m; в) х•18•9; г)k + 271 +209;
д) 704+ 2k + 50; е) 125•х•4•2; е) 10a + 81 + 4а + 40 + а; ж) а + 7 + 2а + 14 + За.
6. Найди значение выражения:
а) 50 • m • 49 • 2, если m = 2; 3, 10; б) 4 • а • 11 • 25, если а = 7; 8; 9; в) m • 27 • 5, если m = 10; 2;
г) 36х + 124 + 16х, если х = 5, 10, 12; д) 16y + 16 • 91, если у = 9.
7. Реши уравнения:
а) (25 + 8) x = 132; б) 181 - 8y = 45; в) 9k-54 = 162; г) 13x + 57 = 330; д) y: 21 = 19; е) х: 34 + 35 = 42;
ё) 8х + 2х - х = 80; ж) 46а - а = 13590.
8. Реши уравнения.
а) 192-Зу = 54-48; б) n • 54 - 34 = 1100; в) х : 12 • 35 = 210; г) 15 • x : 18 = 35; д) 4х + 8х = 204;
е) 4x • 18 • 5 = 0.
9. Реши уравнения:
а) (х-4)(х-5) = 0; б) (х-9)(х-5) = 0; в) (9х-2х): 9 = 14; г) 105: (15х- 10х) = 3; д) (28х-7х + 59): 2 = 250;
е)x:(17574: 87) = 12; е) 20250:(х + 51) = 135; ж) 55481: х-21 = 88; з) 9(152 - 7y) = 927; и) 16(4z-26) = 224.
10. Запиши выражение:
а) произведение числа 8 и суммы а и 13;
б) частное от деления числа 114 на сумму а и b;
в) частное от деления суммы 9 и m на разность 29d и 5.
11. Через 3 часа работы один экскаватор вынул 555 м земли. Сколько кубических метров земли вынет второй экскаватор за 4 часа, если он за час вынимает на 15 м³ больше, чем первый?
12. С двух станций, расстояние между которыми 720 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда 75 км / ч, а второго на 10 км / ч больше. На каком расстоянии друг от друга будут поезда через 4 часа?
13. С одного пункта одновременно в противоположных направлениях выехали два автобуса. Скорость первого - 48 км / ч, скорость второго - на 6 км / ч больше. Через сколько часов расстояние между ними будет равно 510 км?
14. Одновременно из Москвы и Казани вышли два поезда. Через 6 ч они встретились. Поезд из Казани шел со скоростью 71 км / ч. Найди скорость поезда, вышедшего из Москвы, если расстояние между городами 800 км. Какое расстояние между поездами было через 3 часа после отправления?
15. Пассажирский самолет совершил перелет 1200 км за 1 час 40 хе. После короткой посадки его полет продолжался еще 3 ч с той же скоростью. Найди скорость самолета и всё расстояние, которое он пролетел.







