Квадратные уравнения. Готовимся к ОГЭ по математике. Модуль 1. Урок 23

Квадратные уравнения — это уравнения вида $\displaystyle ax^{2}+bx+c=0$, где $x$ — переменная, $a$, $b$ и $c$ — некоторые числа, причём $\displaystyle a\neq 0$.
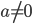Неполные квадратные уравнения — квадратные уравнения, в которых $\displaystyle b=0$ и/или $\displaystyle c=0$. Решение неполных квадратных уравнений рассмотрим на примерах.
Пример 1. Решите уравнение $\displaystyle 4x^{2}+x=0$.
Решение.
В левой части вынесем общий множитель $x$ за скобки:
$\displaystyle x(4x+1)=0$,
$x=0$, или $\displaystyle 4x+1=0$,
        $4x=-1$,
        $x=-0,25$.

$\displaystyle x_{1}=0;$    $\displaystyle x_{2}=-0,25;$ — корни исходного уравнения. Ответ: 0; -0,25.
Пример 2. Решите уравнение $\displaystyle 3x^{2}=81$.
Решение.
$\displaystyle x^{2}=27$,
$\displaystyle x_{1,2}=\pm \sqrt{27},$
$\displaystyle x_{1}=-3\sqrt{3},\; x_{2}=3\sqrt{3}.$
Ответ: $\displaystyle -3\sqrt{3},\; 3\sqrt{3}.$
Пример 3. Решите уравнение $\displaystyle 5x^{2}-20=0.$
Решение.
1-й способ.
Разделим обе части уравнения на 5, получим $\displaystyle x^{2}-4=0$. Замечаем, что в левой части уравнения стоит разность квадратов, поэтому уравнение можно переписать в виде
$\displaystyle x^{2}-2^{2}=0,$
$\displaystyle (x-2)(x+2)=0,$
$\displaystyle x+2=0$ или $\displaystyle x+2=0$,
$\displaystyle x_{1}=-2$    $\displaystyle x_{2}=2$
2-й способ.
$\displaystyle 5x^{2}=20,$
$\displaystyle x^{2}=20:5,$
$\displaystyle x^{2}=4,$
$\displaystyle x_{1,2}=\pm \sqrt{4},$
$\displaystyle x_{1,2}=\pm 2.$
Ответ: —2; 2.
Пример 4. Решите уравнение $\displaystyle 3x^{2}+8=0$.
Решение.
$\displaystyle 3x^{2}+8=0$,
$\displaystyle 3x^{2}=-8$,
$\displaystyle x^{2}=-\frac{8}{3}.$
Квадрат числа не может быть отрицательным, поэтому данное уравнение корней не имеет.
Ответ: корней нет.
Пример 5. Решите уравнение $\displaystyle -1,7x^{2}=0$.
Решение.
Разделим обе части уравнения на —1,7, получим уравнение $\displaystyle x^{2}=0$. Его корнем является только число 0.
Ответ: 0.