Решение квадратных уравнений общего вида. Готовимся к ОГЭ по математике. Модуль 1. Урок 24

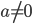Рассмотрим квадратное уравнение общего вида, то есть $\displaystyle ax^{2}+bx+c=0$ , где $\displaystyle a\neq 0$ . Такие уравнения решаем по алгоритму:
• найти дискриминант 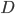$D$ , вычисляемый по формуле $\displaystyle D=b^{2}-4ac$ ;
• по знаку дискриминанта определить число корней уравнения:
— если $\displaystyle D<0$ , то уравнение корней не имеет (что уже можно писать в ответ, дальнейшие вычисления не требуются);
— если $\displaystyle D=0$ , то уравнение имеет один корень $\displaystyle x=-\frac{b}{2a}$ ;
— если $\displaystyle D>0$ , то уравнение имеет два корня:
$\displaystyle x_{1,2}=\frac{-b\pm \sqrt{D}}{2a}$ , то есть
$\displaystyle x_{1}=\frac{-b- \sqrt{D}}{2a},\; x_{2}=\frac{-b+ \sqrt{D}}{2a};$
• найти корни;
• записать ответ.
Пример 1. Решите уравнение $\displaystyle 6x^{2}-13x+2=0$ .
Решение.
$\displaystyle a=6,b=-13,c=2.$
Вычислим дискриминант
$\displaystyle D=b^{2}-4ac.\; D=(-13)^{2}-4\cdot 2\cdot 6=169-48=121,\; D>0,$
поэтому исходное уравнение имеет два корня:
$\displaystyle x_{1,2}=\frac{-b\pm \sqrt{D}}{2a},\; x_{1,2}=\frac{13\pm \sqrt{121}}{2\cdot 6}=\frac{13\pm 11}{12},$
откуда
$\displaystyle x_{1}=\frac{13-11}{12}=\frac{1}{6},\; x_{2}=\frac{13+11}{12}=2.$
Ответ: $\displaystyle \frac{1}{6};2.$
Пример 2. Решите уравнение $\displaystyle 9x^{2}-6x+1=0$ .
Решение.
$\displaystyle a=9,b=-6,c=1.$
Вычислим дискриминант
$\displaystyle D=(-6)^{2}-4\cdot 1\cdot 9=36-36=0.\; D=0,$
поэтому исходное уравнение имеет один корень:
$\displaystyle x=-\frac{b}{2a},\; x=\frac{6}{2\cdot 9}=\frac{1}{3}.$
Ответ: $\displaystyle \frac{1}{3}$ .
Пример 3. Решите уравнение $\displaystyle 3x^{2}-4x+3=0$ .
Решение.
$\displaystyle a=3,b=-4,c=3.$
Вычислим дискриминант
$\displaystyle D=b^{2}-4ac.\; D=(-4)^{2}-4\cdot 3\cdot 3=16-36=-20.\; D<0.$ поэтому исходное уравнение корней не имеет. Ответ: корней нет.