Приведённое квадратное уравнение. Теорема Виета. Готовимся к ОГЭ по математике. Модуль 1. Урок 25

Квадратное уравнение $\displaystyle ax^{2}+bx+c=0$ называется приведённым, если $a=1$.
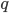Пусть $\displaystyle x^{2}+px+q=0$ — приведённое квадратное уравнение, где $p$ и $q$ — некоторые числа. Если $\displaystyle x_{1}$ и $\displaystyle x_{2}$ — корни уравнения, то справедливы формулы (теорема Виета)
$\displaystyle x_{1}+x_{2}=-p,$
$\displaystyle x_{1}\cdot x_{2}=q.$
Справедливо и обратное утверждение. Если $\displaystyle x_{1}$ и $\displaystyle x_{2}$ — некоторые числа, при этом $\displaystyle x_{1}+x_{2}=-p,\; x_{1}\cdot x_{2}=q$, то уравнение $\displaystyle x^{2}+px+q=0$ имеет корни $\displaystyle x_{1}$ и $\displaystyle x_{2}$, причём других корней нет (теорема, обратная теореме Виета).
Пример 1. Известно, что уравнение $\displaystyle x^{2}+9x-10=0$ имеет корни. Найдите сумму и произведение корней этого уравнения.
Решение. По теореме Виета
$\displaystyle x_{1}+x_{2}=-9,$
$\displaystyle x_{1}\cdot x_{2}=-10.$
Значит, $\displaystyle x_{1}=-10,\; x_{2}=1.$
Ответ: -10; 1.
Пример 2. Составьте квадратное уравнение, корнями которого были бы числа 3 и —5.
Решение.
По теореме Виета,
$\displaystyle x_{1}+x_{2}=-2,$
$\displaystyle x_{1}\cdot x_{2}=-15.$
Напишем приведённое квадратное уравнение, в котором второй коэффициент $\displaystyle p=2$, а свободный член $\displaystyle q=-15$: $\displaystyle x^{2}+2x-15=0.$
По теореме, обратной теореме Виета, числа 3 и —5 являются корнями составленного уравнения.
Ответ: $\displaystyle x^{2}+2x-15=0$.