Прямоугольные координаты в пространстве
Прямоугольная система координат в пространстве состоит из трех взаимно перпендикулярных пересекающихся в одной точке осей, называемых осями координат. Точка пересечения осей называется началом координат и обозначается буквой О. Координатные оси обозначаются через Ох, Оу и Оz и соответственно называются осью абсцисс, осью ординат и осью аппликат.
На каждой оси выбирается положительное направление, указанное стрелкой, и единица меры (е).
Координатные оси Ох, Оу и Oz попарно определяют в пространстве три координатные плоскости хОу, xOz и yOz, пересекающиеся в одной точке О (рис.1).
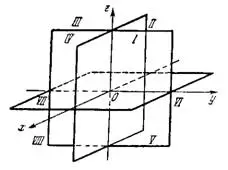
Положение точки М относительно взятых осей определяется отрезками OA, OB, ОС (рис.1), соответственно равными расстояниям точки М от координатных плоскостей. Величины этих отрезков выражаются числами, если измерить их какой-либо единицей меры (е).
Число  — называется абсциссой точки М.
— называется абсциссой точки М.
Число  — называется ординатой точки М.
— называется ординатой точки М.
Число  — называется аппликатой точки М.
— называется аппликатой точки М.
Таким образом, положение любой точки в пространстве определяется тройкой чисел (х,у,z), называемых ее координатами.
Координатные плоскости хОу, хОz и yOz делят пространство на восемь частей, называемых октантами (рис.2).
Координаты точек, расположенных в различных частях, имеют следующие знаки:
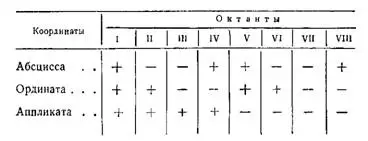
Точки, лежащие на координатных плоскостях, имеют одну из координат, равную 0.
Точки, лежащие на осях координат, имеют две координаты, равные 0.
Начало координат имеет все три координаты, равные 0.
Между тремя числами (х,у,z) и точками пространства устанавливается взаимно однозначное соответствие. Каждой тройке чисел соответствует одна и только одна точка пространства и, наоборот, каждой точке пространства соответствует единственная тройка чисел.







