Решение систем линейных уравнений методом Крамера (примеры)

Рассмотрим систему двух уравнений 1-й степени с двумя неизвестными
$\left\{\begin{matrix} a_{1}x+b_{1}y=c_{1},\\ a_{2}x+b_{2}y=c_{2}. \end{matrix}\right.\; \; (1)$
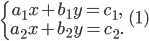
Решение этой системы определяется формулами Крамера:
$\displaystyle x=\frac{\Delta_{x}}{\Delta}, y=\frac{\Delta_{y}}{\Delta},\; \; (2)$
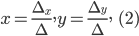
где
$\Delta=\begin{vmatrix} a_{1} & b_{1}\\ a_{2} & b_{2} \end{vmatrix},\; \Delta_{x}=\begin{vmatrix} c_{1} & b_{1}\\ c_{2} & b_{2} \end{vmatrix},\; \Delta_{y}=\begin{vmatrix} a_{1} & c_{1}\\ a_{2} & c_{2} \end{vmatrix}.\;$
Определитель Δ, стоящий в знаменателе, составлен из коэффициентов при неизвестных системы (1), взятых в том же порядке, в каком они стоят в уравнениях, и называется определителем системы.
Определители, стоящие в числителях формул (2), получаются из определителя системы путем замены соответственно первого и второго столбцов свободными членами этой системы.
Пример 1. Решить систему уравнений:
$\left\{\begin{matrix} x+2y=3,\\ 3x-5y=-2. \end{matrix}\right.$
Решение.
$\Delta=\begin{vmatrix} 1 & 2\\ 3 & -5 \end{vmatrix}=-5-6=-11;$
$\Delta_{x}=\begin{vmatrix} \: 3 & \: 2\\ -2 & -5 \end{vmatrix}=-15+4=-11;$
$\Delta_{y}=\begin{vmatrix} 1 & \: 3\\ 3 & -2 \end{vmatrix}=-2-9=-11;$
$x=\frac{\Delta_{x}}{\Delta}=\frac{-11}{-11}=1,\; y=\frac{\Delta_{y}}{\Delta}=\frac{-11}{-11}=1.$
Ответ: (1;1)
Рассмотрим систему трех уравнений 1-й степени с тремя неизвестными
$\left\{\begin{matrix} a_{1}x+b_{1}y+c_{1}z=d_{1},\\ a_{2}x+b_{2}y+c_{2}z=d_{2},\\ a_{3}x+b_{3}y+c_{3}z=d_{3}. \end{matrix}\right.\; \; \; (3)$
Решение этой системы определяется формулами Крамера:
$x=\frac{\Delta_{x}}{\Delta},\; y=\frac{\Delta_{y}}{\Delta},\;z=\frac{\Delta_{z}}{\Delta}, \; (4)$
где
$\Delta=\begin{vmatrix} a_{1} & b_{1} & c_{1}\\ a_{2} & b_{2} & c_{2}\\ a_{3} & b_{3} & c_{3} \end{vmatrix},\; \Delta_{x}=\begin{vmatrix} d_{1} & b_{1} & c_{1}\\ d_{2} & b_{2} & c_{2}\\ d_{3} & b_{3} & c_{3} \end{vmatrix},\; \Delta_{y}=\begin{vmatrix} a_{1} & d_{1} & c_{1}\\ a_{2} & d_{2} & c_{2}\\ a_{3} & d_{3} & c_{3} \end{vmatrix},\; \Delta_{z}=\begin{vmatrix} a_{1} & b_{1} & d_{1}\\ a_{2} & b_{2} & d_{2}\\ a_{3} & b_{3} & d_{3} \end{vmatrix}.\;$
Пример 2. Решить систему:
$\left\{\begin{matrix} \: x-2y+3z=6,\\ 2x+3y-4z=20,\\ 3x-2y-5z=6. \end{matrix}\right.$
Решение.
$\Delta=\begin{vmatrix} 1 & -2 &\: 3 \\ 2 & \: 3 &-4 \\ 3 & -2 & -5 \end{vmatrix}=-15-12+24-27-88-20=-58,$
$\Delta_{x}=\begin{vmatrix} \; 6 & -2 &\: 3 \\ 20 & \; 3 &-4 \\ \; 6 & -2 & -5 \end{vmatrix}=-90+48-120-54-48-200=-464,$
$\Delta_{y}=\begin{vmatrix} 1 & 6 & \; 3 \\ 2 & 20 &-4 \\ 3 & 6 & -5 \end{vmatrix}=-100-72+36-180+24+60=-232,$
$\Delta_{z}=\begin{vmatrix} 1 & -2 & 6 \\ 2 & \; 3 &20 \\ 3 & -2 & 6 \end{vmatrix}=18-120-24-54+24+40=-116,$
$\large x=\frac{\Delta_{x}}{\Delta}=\frac{-464}{-58}=8;\; y=\frac{\Delta_{y}}{\Delta}=\frac{-232}{-58}=4;\; z=\frac{\Delta_{z}}{\Delta}=\frac{-116}{-58}=2.$
Ответ: (8;4;2)