Задача № 1. Привести к простейшему виду уравнение кривой
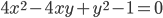
Решение. Разлагая левую часть этого уравнения на линейные множители, будем иметь:
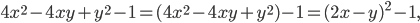
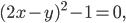
или
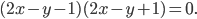
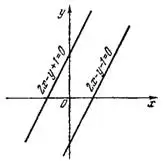
Следовательно, заданная кривая второго порядка распадается на пару параллельных прямых
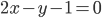 и
и 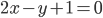 (рис.1).
(рис.1).
Задача № 2.Привести к простейшему виду уравнение кривой 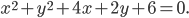
Решение. Данное уравнение не содержит члена с произведением координат.
Собираем в этом уравнении члены, содержащие одно¬именные координаты
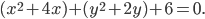
Дополняем выражения в скобках до полных квадратов:
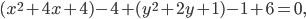
или
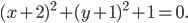
Это уравнение не может иметь места при действительных значениях х и у. Поэтому данное уравнение не определяет никакой линии на плоскости.
Задача № 3. Привести к простейшему виду уравнение
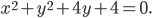
Решение. Данное уравнение может быть записано так:
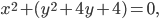 или
или 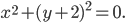
Это равенство имеет место только при х = 0 и у = -2. Поэтому данное уравнение определяет на плоскости одну точку (0; -2).
Решения этих задач подробно изложено в следующем видео







