Рассмотрим уравнение х+у=3, связывающее абсциссу х и ординату у. Ему удовлетворяет множество пар значений х, у, например, х=1 и у=2, х=2 и у=1, х=3 и у=0,x=4 и у=—1 и т. д. Каждой паре координат (в данной системе координат) соответствует одна точка.
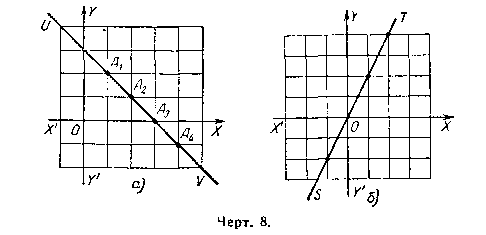 На черт. 8, в изображены точки A1(1; 2), A1(2; 1), A3(3; 0), A4(4; —1). Они лежат на одной прямой UV. На той же прямой лежит всякая другая точка, координаты которой удовлетворяют уравнению х+у=3. Обратно, у любой точки, лежащей на прямой UV, координаты х, у удовлетворяют уравнению х+у=3.
На черт. 8, в изображены точки A1(1; 2), A1(2; 1), A3(3; 0), A4(4; —1). Они лежат на одной прямой UV. На той же прямой лежит всякая другая точка, координаты которой удовлетворяют уравнению х+у=3. Обратно, у любой точки, лежащей на прямой UV, координаты х, у удовлетворяют уравнению х+у=3.
Сообразно с этим говорят: уравнение х+у=3 есть уравнение прямой линии UV. Говорят также: уравнение x + y = 3 представляет прямую UV. В аналогичном  смысле надо понимать выражения: «уравнение прямой линии ST (черт. 8, б) есть у = 2х, уравнение х² + y² = 49 представляет окружность (черт. 9), радиус которой содержит 7 масштабных единиц, а центр совмещается с началом координат. Вообще, уравнение, связывающее координаты х, у, называется уравнением линии L, если соблюдены два условия: 1) координаты х, у всякой точки М линии L удовлетворяют этому уравнению, 2) координаты х, у всякой точки, не лежащей на линии L, не удовлетворяют этому уравнению.
смысле надо понимать выражения: «уравнение прямой линии ST (черт. 8, б) есть у = 2х, уравнение х² + y² = 49 представляет окружность (черт. 9), радиус которой содержит 7 масштабных единиц, а центр совмещается с началом координат. Вообще, уравнение, связывающее координаты х, у, называется уравнением линии L, если соблюдены два условия: 1) координаты х, у всякой точки М линии L удовлетворяют этому уравнению, 2) координаты х, у всякой точки, не лежащей на линии L, не удовлетворяют этому уравнению.
Координаты точки М, взятой на линии L произвольным образом, называют текущими координатами, так как линия Z может быть образована перемещением («течением») точки М. Пусть M1, М2, М3, . . . (черт. 10) — последовательные положения точки М на линии L.
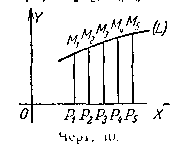
Построим ряд перпендикуляров M1P1, М2Р2. М3P3.. . . . к оси ОХ. Получим идущие друг за другом отрезки P1M1, Р2М2, Р3M3, ... На оси ОХ отсекаются при этом отрезки ОР1, ОР2, ОР3,. . . . Они будут абсциссами. С этим связано происхождение терминов «абсцисса» и «ордината». Латинское слово «абсцисса» (abscissa) в переводе означает «отсеченная»; слово «ордината» есть сокращение термина «ординатим дукта» (ordinatim ducta), что означает «подряд проведенная».
Представляя каждую точку плоскости ее координатами, а каждую линию уравнением,
связывающим текущие координаты, мы сводим геометрическую задачу к «аналитической» (т. е. вычислительной). Отсюда название "аналитическая геометрия".
Уравнение линии







