Уравнением прямой называется такое уравнение первой степени с переменными х и у, которому удовлетворяют координаты любой точки этой прямой. Уравнение вида
![]()
называется общим уравнением прямой.
Уравнение прямой, разрешенное относительно переменной у, т. е. уравнение вида
![]()
называется уравнением с угловым коэффициентом. Параметр k называется угловым коэффициентом и равен тангенсу угла наклона прямой к оси Ox, k= tg φ.
Параметр b — величина отрезка, отсекаемая прямой (2) на оси Оу, считая от начала координат.
Уравнение вида
![]()
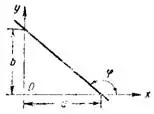
где а и b — величины отрезков, отсекаемых прямой на осях координат (рис. 1), называется уравнением прямой в отрезках.
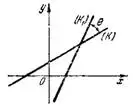
Углом между двумя прямыми y=kx+b и y=k₁x+b₁ называется угол, на который надо повернуть прямую (с угловым коэффициентом k) до совпадения ее со второй прямой (с угловым коэффициентом k₁), против часовой стрелки (рис. 2).
Этот угол вычисляется по формуле:
![]()
Условие параллельности двух прямых
![]()
Условие перпендикулярности двух прямых:
![]()
Если прямые даны уравнениями в общем виде
![]()
то условием параллельности будет равенство
![]()
а перпендикулярности
![]()
Если прямая имеет угловой коэффициент k и проходит через данную точку то ее уравнение имеет вид:
![]()
Если в этом уравнении параметру k давать различные значения, то будем получать всевозможные прямые, проходящие через данную точку (х₁,у₁). Тогда уравнение (7) дает пучок прямых с центром в точке (х₁,у₁).
Если прямая проходит через две данные точки (х₁,у₁) и (х₂,у₂), то уравнение
![]()
называется уравнением прямой, проходящей через две данные точки.
Условием того, что три данные точки (х₁,у₁), (х₂,у₂) и (х₃,у₃) лежат на одной прямой, служит равенство:
![]()
Если две прямые даны общими уравнениями:
![]()
то координаты точки пересечения их определяются путем совместного решения этих уравнений:
![]()
Если ![]() то прямые имеют точку пересечения.
то прямые имеют точку пересечения.
Если ![]() то прямые параллельны и не имеют точки пересечения.
то прямые параллельны и не имеют точки пересечения.
Если ![]() то прямые совпадают и точка их пересечения становится неопределенной.
то прямые совпадают и точка их пересечения становится неопределенной.
Уравнение вида
![]()
называется уравнением пучка прямых, проходящих через точку пересечения двух данных прямых:
![]()
Уравнение вида
![]()
называется нормальным уравнением прямой.
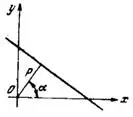
р — длина перпендикуляра (нормали), опущенного из начала координат на прямую, α — угол наклона этого перпендикуляра к оси Ох (рис. 3).
Всякое уравнение прямой общего вида Ах+Ву+С=0 можно привести к нормальному виду, умножая все его члены на нормирующий множитель.
![]()
взятый со знаком, противоположным знаку свободного члена С.
Отклонение δ данной точки от данной прямой есть длина перпендикуляра, опущенного из этой точки на прямую, взятая со знаком плюс, если точка и начало координат лежат по разные стороны от прямой, и со знаком минус, если они лежат по одну сторону от прямой.
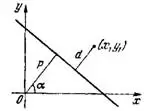
Чтобы найти отклонение точки М(х₁,у₁) от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки х₁ и у₁:
![]()
или
![]()
Для точек, лежащих на прямой, отклонение равно нулю. Расстояние d от точки до прямой есть абсолютная величина отклонения этой точки от прямой:
![]()
или
![]()
Положение прямой в полярной системе координат определяется длиною перпендикуляра р, опущенного из полюса на прямую, и углом α, образованным этим перпендикуляром и полярной осью ОР (рис. 5).
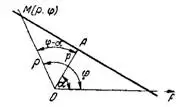
Уравнение прямой в полярных координатах имеет вид
р = ρcos(φ-α) (16)







