Если натуральное число а не делится на натуральное число Ь, то не существует такого натурального числа с, что а = Ь • с. В этом случае говорят о делении с остатком. Так, при делении 51 на 8 в частном получается 6 и в остатке 3, таким образом, 51=8•6+3 или 51/8=6+3/8. В общем случае можем записать: если а — делимое, b — делитель (a>b), р — частное, r — остаток , то a = b•p + r, где r<b. Иначе можно записать: а / b = р + r/b. Здесь a, b, р, r — натуральные числа (если а делится на b без остатка, то r = 0, т. е. r не является натуральным числом). В частности, запись a = 5 р + 3 означает, что при делении числа а на 5 получается число р и остаток 3.
Пример. Найти частное и остаток от деления числа 587 на число 31.
Решение.
Выполняем деление «углом»:
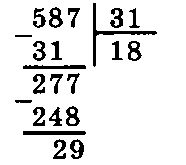
В результате деления получаем частное 18, остаток 29. Можем записать: 587 = 18•31+29 или 587/31=18+29/31.
Ответ: частное = 18, остаток = 29.
Деление с остатком. Квадрат и куб числа






