Задача 1. Сумма трех чисел, составляющих арифметическую прогрессию, равна 30. Если из второго члена этой прогрессии вычесть число 2, а остальные числа оставить без изменения, то получится геометрическая прогрессия. Найти эти числа.
Решение. Пусть 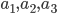 — члены арифметической прогрессии;
— члены арифметической прогрессии; 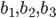 — члены геометрической прогрессии. По условию
— члены геометрической прогрессии. По условию 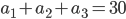 . Найдем связь между
. Найдем связь между 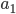 и
и 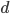 — разностью прогрессии.
— разностью прогрессии.


Выразим все члены прогрессии через 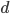 :
:  . Таким образом,
. Таким образом, 
По условию  Тогда
Тогда  — геометрическая прогрессия.
— геометрическая прогрессия.
Поскольку

Тогда
 или
или  .
.Отсюда получаем две тройки чисел: 4;10;1б (
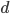 =6) и 16;10;4(
=6) и 16;10;4(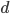 =-6).
=-6).Ответ: 4;10;16 или 16;10;4.
Задача 2. Четыре числа составляют геометрическую прогрессию. Если из первого числа вычесть 11, из второго 1, Из третьего 3, а из четвертого 9, то получится арифметическая прогрессия. Найти эти числа.
Решение. Обозначим искомые числа через  — четыре первых члена геометрической прогрессии. Пусть
— четыре первых члена геометрической прогрессии. Пусть  — соответствующие члены арифметической прогрессии. Ясно, что
— соответствующие члены арифметической прогрессии. Ясно, что 
Тогда

Применим характеристическое свойство арифметической прогрессии:

Тогда получаем систему уравнений, в которой неизвестными будут
 и
и 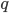 :
:
Запишем геометрическую прогрессию:

Ответ: 27;9;3;1.






