Множества бывают конечные и бесконечные. Конечное множество можно задать перечислением всех его элементов. Бесконечные множества определяются при помощи свойств. При задании таких множеств выписывается или несколько первых элементов, или записывают элемент и свойство, которым обладают элементы данного множества.
Пример 1. А ={зима, весна, лето, осень} — множество времен года, конечное множество.
Пример 2. Z ={0;±1;±2;...} — множество всех целых чисел, бесконечное множество.
Пример 3. {2n| nєZ} - множество всех четных чисел, бесконечное множество.
Пример 4. {2n+1| nєZ} — множество всех нечетных чисел, бесконечное множество.
Множество А называется подмножеством множества В, если каждый элемент множества А принадлежит множеству В. Записывается это так:
![]()
Иногда читают так: А содержится в В или В содержит А. На рис. 3 множество А изображено внутри множества В.
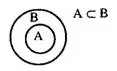
Рис. 3
Пример 1. Множество всех четных положительных чисел есть подмножество множества всех натуральных чисел.
Из определения множества следует, что любое множество является подмножеством самого себя, т.е. справедливо включение
![]()
Полагают по определению, что пустое множество является подмножеством любого множества, т.е. для любого А: ᴓєА.
Заметим, что множество из n элементов содержит 2ⁿ подмножеств.
Пример 2. Выписать все подмножества множества А, состоящего из трех элементов, А = {а;Ь;с}.
Решение.
Всех подмножеств будет 2³=8. Это такие подмножества:
{a;b;c}, {a;b}, {а;с}, {b;с}, {а}, {Ь}, {с}, ᴓ.
Множества А и В называются равными (записывается А = В), если АсВ и ВсА. Равные множества состоят из одних и тех же элементов.
Примеры равных множеств:
Пример 3.
![]()
Пример 4.
![]()
Конечные и бесконечные множества. Подмножества






