Линейные неравенства и неравенства, приводимые к линейным
Линейным неравенством с одной переменной называется неравенство вида (или 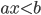 ,
, 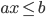 ,
, 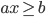 ). Если , то неравенство .
). Если , то неравенство .
Если 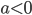 , то неравенство . Если
, то неравенство . Если 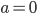 , то неравенство принимает вид и оно верно для любого
, то неравенство принимает вид и оно верно для любого 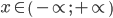 , если
, если 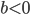 , и не имеет решений, если .
, и не имеет решений, если .
Пример 1. Решить неравенство .
Решение.
Ответ:

Пример 2. Решить неравенство
 .
.Решение.

Ответ:

Неравенствами, приводимыми к линейным, назовем следующие неравенства: (или
 ,
,  ,
,  ), (или
), (или  ,
,  ,
,  ).
).У этих неравенств левая и правая части представляют собой линейные функции относительно х. Такие неравенства в процессе преобразований сводятся к линейным.
Пример 3. Решить неравенство
 .
.Решение.
![2x+3\leq x-8\Leftrightarrow 2x-x\leq -3-8\Leftrightarrow x\leq -11\Leftrightarrow x\in (-\propto ;-11].](https://math-helper.ru/wp-content/plugins/latex/cache/tex_61c4ccc94c6922718e09063171ef4a84.gif)
Ответ:
![x\in (-\propto ;-11].](https://math-helper.ru/wp-content/plugins/latex/cache/tex_4f6577a12d5239d3ee6377476fa9bfca.gif)
Пример 4. Решить неравенство
Решение.

 , так как при делении на отрицательное число нужно изменить знак на противоположный.
, так как при делении на отрицательное число нужно изменить знак на противоположный.Ответ:

Пример 5. Решить неравенство

Решение. Рассмотрим несколько форм записи решения исходного неравенства.
1-я форма записи.


В процессе решения неравенства мы привели левую и правую части исходного неравенства к общему знаменателю, то есть к числу 6, а затем применили теоремы о равносильных неравенствах.
2-я форма записи.


В процессе решения мы вначале умножили обе части исходного неравенства на 6, а затем применили свойства неравенств (теоремы о равносильных неравенствах).
3-я форма записи.


В процессе решения исходного неравенства с самого начала все неизвестные были перенесены в левую часть неравенства, а в правой части остались только постоянные. Далее выражение слева было приведено к общему знаменателю, а затем использованы теоремы о равносильных неравенствах.
Ответ: 
Замечание. Ответы к неравенствам не обязательно давать с применением теории множеств. Так, вполне допустимо дать ответ в виде .






