Дифференциал функции. Практикум по математическому анализу. Урок 39

Из определений производной $\displaystyle y'=\underset{\Delta x\rightarrow 0}{\textrm{lim}}\frac{\Delta y}{\Delta x}$ и предела переменной следует, что $\displaystyle \frac{\Delta y}{\Delta x}=y'+\varepsilon$ или $\displaystyle \Delta y=y'\Delta x+\varepsilon \Delta x$, где $\displaystyle \varepsilon \to 0$ при $\displaystyle \Delta x \to 0$, т. е. что приращение функции можно разбить на две части.
Главная часть приращения функции, линейная относительно приращения независимой переменной, называется дифференциалом функции и обозначается знаком 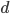$d$:

$\displaystyle dy=y'\Delta x.$

Дифференциал независимой переменной $x$ равен ее приращению, $dx=\Delta x$. Поэтому

$dy=y'dx,\; \; \; \; \; \; (a)$

т. е. дифференциал функции равен ее производной, умноженной на дифференциал независимой переменной.
Для всякой данной функции $y=f(x)$ производная $y'$ зависит только от одной переменной $x$, тогда как ее дифференциал $dy$ зависит от двух независимых друг от друга переменных: $x$ и $\Delta x$.
Нахождение дифференциала функции называется дифференцированием, так же как и нахождение производной, так как согласно формуле (а), чтобы найти дифференциал какой-либо функции, надо найти производную этой функции и умножить ее на дифференциал независимой переменной.
Формула (а) верна и в случае, если у есть сложная функция, т. е. если $x$ есть функции переменной $t$.
При достаточно малых значениях $\left | dx \right |$ приращение функции может быть заменено ее дифференциалом с как угодно малой относительной ошибкой:

$\Delta y\approx dy,$

исключая точки, в которых $y'=0$.
Это приближенное равенство применяется для приближенных вычислений, так как вычисление дифференциала функции значительно проще, чем вычисление ее приращения.
Пример 1. Найти дифференциалы функций:
1) $y=x^{3}-3^{x}$; 2) $\displaystyle F(\varphi )=\cos \frac{\varphi }{3}+\sin \frac{3}{\varphi }$;
3) $\displaystyle z=\textrm{ln}(1+e^{10x})+\textrm{arcctg}e^{5x}$; вычислить $\displaystyle dz|_{x=0;dx=0,1.}$
Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим
искомый дифференциал данной функции:
1) $\displaystyle dy=y'dx=(x^{3}-3^{x})'dx=(3x^{2}-3^{x}\textrm{ln}3)dx$;
2) $\displaystyle dF(\varphi )=d\left ( cos\frac{\varphi }{3}+\sin \frac{3}{\varphi } \right )=\left ( cos\frac{\varphi }{3}+\sin \frac{3}{\varphi } \right )'d\varphi =$
$\displaystyle =\left [ -\sin \frac{\varphi }{3}\cdot \left ( \frac{\varphi }{3} \right )'+\cos \frac{3}{\varphi }\cdot \left ( \frac{3}{\varphi } \right )' \right ]d\varphi =-\left ( \frac{1}{3}\sin \frac{\varphi }{3}+\frac{3}{\varphi ^{2}}\cos \frac{3}{\varphi } \right )d\varphi ;$
3) $\displaystyle dz=\left [ \frac{(1+e^{10x})'}{1+e^{10x}} - \frac{(e^{5x})'}{1+e^{10x}}\right ]dx= \left ( \frac{10e^{10x}}{1+e^{10x}}-\frac{5e^{5x}}{1+e^{10x}} \right )dx=\frac{5e^{5x}(2e^{5x}-1)}{1+e^{10x}}dx$.
Полагая $x=0$ и $dz=0,1$, получим $dz=0,25$.