Геометрические вероятности. Решение типовых задач. Часть 2
Задача №1. Задача о встрече. Два товарища условились встретиться в определенном месте между 12 часами и половиной первого дня. Пришедший первым ждет другого в течение 20 минут, после чего уходит. Найти вероятность того, что встреча товарищей состоится, если каждый из них наудачу выбирает момент своего прихода (в промежутке от 12 часов до половины первого) и моменты прихода обоих независимы.
Решение. Обозначим событие: А - встреча товарищей состоится.
Найдем вероятность события А, применив формулу (1). Обозначим момент прихода одного из них через х мин., а момент прихода другого через у, мин. Для того, чтобы встреча произошла, необходимо и достаточно, чтобы выполнялось условие: 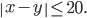
Будем изображать х и у как декартовы координаты точек плоскости; в качестве единицы масштаба выберем минуту (рис.1).
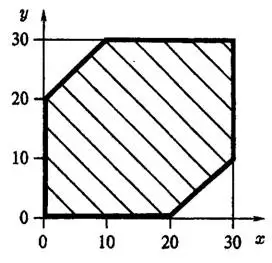
Все возможные исходы испытания изображаются точками фигуры, ограниченной квадратом, сторона которого равна 30; площадь этого квадрата равна 
Неравенство  равносильно системе неравенств:
равносильно системе неравенств:

Исходы испытания, благоприятствующие событию А, удовлетворяют системе неравенств:

Решениями этой системы неравенств являются координаты всех точек плоскости, расположенных на рис. 1 в заштрихованной области, то есть между граничными прямыми:
 и на самих граничных прямых. Точки плоскости, принадлежащие заштрихованной области, характеризуют исходы испытания, благоприятствующие событию А. Площадь заштрихованной фигуры равна
и на самих граничных прямых. Точки плоскости, принадлежащие заштрихованной области, характеризуют исходы испытания, благоприятствующие событию А. Площадь заштрихованной фигуры равна 
Искомая вероятность события А равна отношению площади заштрихованной фигуры к площади всего квадрата:

Задача №2. Коэффициенты р и q квадратного уравнения
 выбирают наудачу в промежутке (0; 2). Какова вероятность того, что корни этого уравнения будут действительными числами?
выбирают наудачу в промежутке (0; 2). Какова вероятность того, что корни этого уравнения будут действительными числами?Решение. Обозначим событие: А - корни данного уравнения будут действительными числами.
Найдем вероятность события А, применив формулу (1). Пусть коэффициены р и q квадратного уравнения - наудачу взятые числа. Их возможные значения:
 Представим p и q как прямоугольные декартовы координаты точек плоскости. Возможные значения р и q в системе координат Opq будут представлены точками, расположенными внутри и на границах представленного на рис.2 квадрата, площадь которого
Представим p и q как прямоугольные декартовы координаты точек плоскости. Возможные значения р и q в системе координат Opq будут представлены точками, расположенными внутри и на границах представленного на рис.2 квадрата, площадь которого 
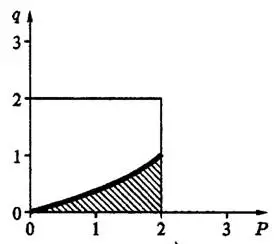
Корни квадратного уравнения являются действительными числами в том случае, когда дискриминант D этого уравнения неотрицателен.
Поэтому благоприятствующие событию А исходы испытания удовлетворяют условию:  откуда следует, что
откуда следует, что 
Построим границы области, которой принадлежат точки плоскости, удовлетворяющие условиям:

Граничные прямые
 являются сторонами квадрата, ограничивающего область возможных значений р и q. Граничная кривая
являются сторонами квадрата, ограничивающего область возможных значений р и q. Граничная кривая  представляет собой параболу. Решениями составленной системы неравенств являются координаты всех точек плоскости, расположенных на рис.2 в заштрихованной области, то есть между граничными линиями
представляет собой параболу. Решениями составленной системы неравенств являются координаты всех точек плоскости, расположенных на рис.2 в заштрихованной области, то есть между граничными линиями  и на самих этих линиях. Точки
и на самих этих линиях. Точкиплоскости, принадлежащие заштрихованной области, характеризуют исходы испытания, благоприятствующие событию А. Площадь заштрихованной области равна

Вероятность события А равна








