Теорема сложения вероятностей двух несовместных событий:
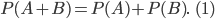
В этой формуле: P(A+B) - вероятность суммы двух несовместных событий А и В, т.е. вероятность наступления одного из этих двух событий; Р(А) - вероятность наступления
события А; Р(В) - вероятность наступления события В; Р(А) + Р(В) - сумма вероятностей событий А и В.
Если  - n попарно несовместных событий, то
- n попарно несовместных событий, то

Если
 - n несовместных событий, образующих полную группу, то
- n несовместных событий, образующих полную группу, то
Если А и
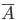 - два несовместных события, образующих полную группу, то
- два несовместных события, образующих полную группу, то 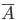 - событие, противоположное событию А, Вероятность события
- событие, противоположное событию А, Вероятность события 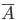 равна
равна
Теорема умножения вероятностей:

В этой формуле Р(АВ) - вероятность произведения двух зависимых событий A и B, т. е. вероятность их совместного наступления; Р(А) - вероятность события А;
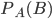 - условная вероятность события В, вычисленная в предположении, что событие А уже наступило;
- условная вероятность события В, вычисленная в предположении, что событие А уже наступило;  - произведение вероятности события А на условную вероятность
- произведение вероятности события А на условную вероятность 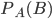 .
.В частности, для двух независимых событий А и В:

В этой формуле Р(АВ) - вероятность произведения двух независимых событий А и B, т, е. вероятность их совместного наступления (наступления и события А, и события В), Р(А) - вероятность события А, Р(В) - вероятность события В;
 - произведение вероятностей событий A и В.
- произведение вероятностей событий A и В.Если
 - n зависимых событий, то
- n зависимых событий, то
в этой формуле
 - вероятность произведения событий
- вероятность произведения событий  , т.е. вероятность их совместного наступления;
, т.е. вероятность их совместного наступления;  - условная вероятность события
- условная вероятность события  , вычисленная в предположении, что событие
, вычисленная в предположении, что событие  наступило;...,
наступило;...,  - вероятность события
- вероятность события  , вычисленная в предположении, что все предыдущие n-1 события наступили. В частности, для n независимых событий
, вычисленная в предположении, что все предыдущие n-1 события наступили. В частности, для n независимых событий  :
:
где
 - вероятность произведения событий
- вероятность произведения событий  ;
; - произведение вероятностей этих событий.
- произведение вероятностей этих событий.






