Задача №1. В денежно-вещевой лотерее на каждые 1000 билетов приходится 5 денежных и 20 вещевых выигрышей. Какова вероятность выигрыша на один билет?
Решение. Рассмотрим события:
 - вещевой выигрыш по одному билету;
- вещевой выигрыш по одному билету;
 - денежный выигрыш по одному билету;
- денежный выигрыш по одному билету;
 - любой выигрыш по одному билету.
- любой выигрыш по одному билету.
 и
и  - несовместные события. Событие А состоит в том, что произойдет или событие
- несовместные события. Событие А состоит в том, что произойдет или событие  , или событие
, или событие  (безразлично, какое); это означает, что событие А является суммой событий
(безразлично, какое); это означает, что событие А является суммой событий  и
и  :
: 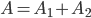 . Найдем вероятности событий
. Найдем вероятности событий  и
и  , применив формулу (1):
, применив формулу (1):

Вероятность события А найдем по теореме сложения вероятностей несовместных событий. Согласно формуле (8) искомая вероятность равна

Задача №2. За ответ на экзамене ученик может получить одну из следующих оценок: 5, 4, 3, 2. Вероятность того, что ученик получит оценку 5, равна 0,3; оценку 4 - 0,4; оценку 3 - 0,2 и оценку 2 - 0,1. Какие из названных событий составляют полную группу несовместных событий? Какое событие противоположно событию: «ученик получит оценку 5» и какова вероятность этого события?
Решение. Рассмотрим события:
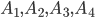 - Ученик получит, соответственно, оценку: 5,4,3,2;
- Ученик получит, соответственно, оценку: 5,4,3,2;А - ученик получит какую-то из этих оценок: или 5, или 4, или 3, или 2.
Вероятности событий
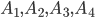 равны:
равны: 
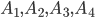 - несовместные события, составляющие полную группу. Событие А представляет собой сумму этих событий:
- несовместные события, составляющие полную группу. Событие А представляет собой сумму этих событий: , Событие А - достоверное;
, Событие А - достоверное; 
Событию
 - ученик получит оценку 5, противоположно событие
- ученик получит оценку 5, противоположно событие  - ученик не получит оценку 5. По формуле (11) найдем:
- ученик не получит оценку 5. По формуле (11) найдем: 
Задача №3. Контрольная работа по математике оценивается целым числом баллов, причем наибольшее число баллов равно 10. Вероятность получить студенту N за эту работу 10 баллов равна 0,2; 9 баллов - 0,3 и от 1 до 9 баллов включительно - 0,7. Найти вероятность того, что студент N получит
а) не менее 9 баллов,
б) ноль баллов.
Решение. Рассмотрим события:
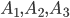 - студент получит, соответственно: 10 баллов; 9 баллов; от 1 до 9 баллов включительно;
- студент получит, соответственно: 10 баллов; 9 баллов; от 1 до 9 баллов включительно;А - студент получит не менее 9 баллов;
В - студент получит 0 баллов.
Вероятности событий
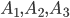 равны:
равны: 
Обратим внимание на то, что
 и
и 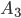 - совместные события. В этой задаче и далее будем находить суммы только несовместных событий и применять теорему сложения вероятностей только для таких событий.
- совместные события. В этой задаче и далее будем находить суммы только несовместных событий и применять теорему сложения вероятностей только для таких событий.а) Событие А состоит в том, что студент получит или 9, или 10 баллов; это означает, что А является суммой событий
 и
и  . События
. События  и
и  - несовместные;
- несовместные; 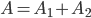 .
.Найдем вероятность события А, воспользовавшись формулой (8):

б) Рассмотрим событие
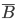 , противоположное событию
, противоположное событию  :
: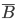 - студент не получит 0 баллов.
- студент не получит 0 баллов.Событие
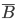 состоит в том, что студент получит или 10 баллов, или от 1 до 9 баллов включительно. Это означает, что
состоит в том, что студент получит или 10 баллов, или от 1 до 9 баллов включительно. Это означает, что 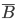 является суммой двух несовместных событий
является суммой двух несовместных событий  и
и 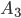 :
:  .
.Найдем вероятность события
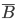 , применив формулу (8):
, применив формулу (8):
Вероятность события В найдем по формуле (11):








